题目内容
【题目】已知函数
，
是奇函数．
（1）求
，
的值；
（2）证明：
是区间
上的减函数；
（3）若
，求实数
的取值范围．
【答案】（1）
，
；（2）见解析；（3）
【解析】
（1）由于函数
是奇函数，且
有意义，则
，定义域关于原点对称，列出方程，即可得到
，
；（2）运用单调性的定义，注意作差、变形，同时运用指数函数的单调性，即可判断符号，得到结论成立；（3）运用奇函数的定义和函数是区间
上的减函数，得到不等式组，注意定义域的运用，解出它们即可得到范围．
（1）∵函数
，
是奇函数，
∴
，且
，
即，.
（2）证明：由（1）得
，
，
设任意
且
，
∴
，
∵，∴
，∴
，
又∵
，
，
∴
，∴
.
∴是区间上的减函数．
（3）∵
，
∴
，
∵奇函数，∴
，
∵是区间上的减函数，
∴
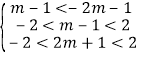即有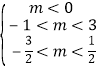
，
∴
，
则实数
的取值范围是
.
练习册系列答案
相关题目
【题目】为了研究“晚上喝绿茶与失眠”有无关系，调查了100名人士，得到下面的列联表：
失眠 | 不失眠 | 合计 | |
晚上喝绿茶 | 16 | 40 | 56 |
晚上不喝绿茶 | 5 | 39 | 44 |
合计 | 21 | 79 | 100 |
由已知数据可以求得：
，则根据下面临界值表：
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
可以做出的结论是（ ）
A. 在犯错误的概率不超过0.01的前提下认为“晚上喝绿茶与失眠有关”
B. 在犯错误的概率不超过0.01的前提下认为“晚上喝绿茶与失眠无关”
C. 在犯错误的概率不超过0.05的前提下认为“晚上喝绿茶与失眠有关”
D. 在犯错误的概率不超过0.05的前提下认为“晚上喝绿茶与失眠无关”
