题目内容

已知F1，F2为椭圆
x2
4
+y2=1的两个焦点，并且椭圆上点P满足∠F1PF2=90°，则△F1PF2的面积为______．
由椭圆的方程可得a=2，b=1，c=
3
，
令|F1P|=m、|PF2|=n，由椭圆的定义可得m+n=2a=4 ①，
Rt△F1PF2 中，由勾股定理可得（2c）2=m2+n2，
∴m2+n2=12②，
由①②可得m•n=2，
∴△F1PF2的面积是
1
2
m•n=1．
故答案为：1．
练习册系列答案
相关题目
已知椭圆
x2
16
+
y2
12
=1上一点P到焦点F1的距离等于3，那么点P到另一焦点F2的距离等于______．
椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）的左、右焦点分别是F1，F2，过F2作倾斜角为120°的直线与椭圆的一个交点为M，若MF1垂直于x轴，则椭圆的离心率为（　　）
A．
12-2
3
11
B．2-
3
C．2（2-
3
）		D．
3
3
已知椭圆的中心在原点，一个焦点与抛物线y2=8x的焦点重合，一个顶点的坐标为
0，2
，则此椭圆方程为______．
已知椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的离心率为e=
2
2
，左、右焦点分别为F1、F2，点P的坐标为（2，
3
），且F2在线段PF1的中垂线上．
（Ⅰ）求椭圆C的方程；
（Ⅱ）如果圆E：（x-
1
2
）2+y2=r2被椭圆C所覆盖，求圆的半径r的最大值．
21、已知|
EF
|=2c，|
EF
|=2a（a＞c），2
EH
=
EG
，2
EO
=
EF
，
HP
•
EG
=0（G为动点）（a＞c）．
（1）建立适当的平面直角坐标系，求出点P的轨迹方程；
（2）若点P的轨迹上存在两个不同的点A、B，且线段AB的中垂线与EF（或EF的延长线）有唯一的交点C，证明：|
OC
|＜
c2
a
．
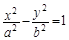已知双曲线(a＞0，b＞0)的一条渐近线与圆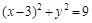相交于A，B两点，若|AB|=2，则该双曲线的离心率为(      )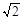
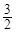
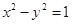A．8B．2C．3D．
双曲线的顶点到其渐近线的距离等于  （　　）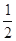
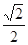
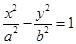A．B．C．1D．
已知双曲线C ：的焦距为10 ，点P （2,1）在C 的渐近线上，
则C的方程为（　　）
A．B．C．D．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网