题目内容
已知椭圆C:
+
=1(a>b>0)的离心率为e=
,左、右焦点分别为F1、F2,点P的坐标为(2,
),且F2在线段PF1的中垂线上.
(Ⅰ)求椭圆C的方程;
(Ⅱ)如果圆E:(x-
)2+y2=r2被椭圆C所覆盖,求圆的半径r的最大值.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| 3 |
(Ⅰ)求椭圆C的方程;
(Ⅱ)如果圆E:(x-
| 1 |
| 2 |
(1)椭圆C的离心率e=
,得
=
,
其中c=
,椭圆C的左、右焦点分别为F1(-c,0),F2(c,0),又点F2在线段PF1的中垂线上,
∴|F1F2|=|PF2|,∴(2c)2=(
)2+(2-c)2,
解得c=1,a2=2,b2=1,
∴椭圆C的方程为
+y2=1.
(2)设P(x0,y0)是椭圆C上任意一点,
则
+
=1,|PE|=
,∵
=1-
,
∴|PE|=
=
(-
≤
≤
).
当x0=1时,|PE|min=
=
,
∴半径r的最大值为
.
| ||
| 2 |
| c |
| a |
| ||
| 2 |
其中c=
| a2-b2 |
∴|F1F2|=|PF2|,∴(2c)2=(
| 3 |
解得c=1,a2=2,b2=1,
∴椭圆C的方程为
| x2 |
| 2 |
(2)设P(x0,y0)是椭圆C上任意一点,
则
| ||
| 2 |
| y | 20 |
(
|
| y | 20 |
| ||
| 2 |
∴|PE|=
(
|
|
| 2 |
| x | 0 |
| 2 |
当x0=1时,|PE|min=
|
| ||
| 2 |
∴半径r的最大值为
| ||
| 2 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

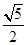
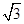
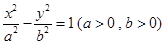 的两顶点为A1,A2,虚轴两端点为B1,B2,两焦点为F1,F2.若以A1A2为直径的圆内切于菱形F1B1F2B2,切点分别为A,B,C,D,则该双曲线的离心率e= .
的两顶点为A1,A2,虚轴两端点为B1,B2,两焦点为F1,F2.若以A1A2为直径的圆内切于菱形F1B1F2B2,切点分别为A,B,C,D,则该双曲线的离心率e= .