题目内容

已知椭圆的中心在原点，一个焦点与抛物线y2=8x的焦点重合，一个顶点的坐标为
0，2
，则此椭圆方程为______．
抛物线y2=8x的焦点为F（2，0），
∵椭圆的中心在原点，一个焦点与抛物线y2=8x的焦点重合，
∴F（2，0）为椭圆的右焦点，
设椭圆的方程为
x2
a2
+
y2
b2
=1（a＞b＞0），
∵椭圆的一个顶点的坐标为
0，2
，且c=2．
∴
c=
a2-b2
=2
b=2
，
解得a2=8且b2=4，
∴椭圆的方程为
x2
8
+
y2
4
=1．
故答案为：
x2
8
+
y2
4
=1
练习册系列答案
相关题目
动点P为椭圆
x2
25
+
y2
16
=1上任意一点，左右焦点分别是F1，F2，直线l为∠F1PF2的外角平分线，过F1作直线l的垂线，垂足为Q，则点Q的轨迹方程是（　　）
A．x2+y2=25B．x2+y2=16C．x2-y2=25D．x22y2=16
椭圆2x2+3y2=6的焦距是（　　）
A．2(
3
-
2
)		B．2C．2
5
D．2(
3
+
2
)
已知椭圆的方程为
x2
9
+
y2
4
=1，则该椭圆的长半轴长为（　　）
A．3B．2C．6D．4
曲线
x2
4
+
y2
3
=1与曲线
x2
4-k
+
y2
3-k
=1（k＜3）的（　　）
A．长轴长相等B．短轴长相等C．离心率相等D．焦距相等
如图，抛物线形拱桥的顶点距水面4m时，测得拱桥内水面宽为16m；当水面升高3m后，拱桥内水面的宽度为______m．
已知F1，F2为椭圆
x2
4
+y2=1的两个焦点，并且椭圆上点P满足∠F1PF2=90°，则△F1PF2的面积为______．
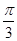如图所示，双曲线的中心在坐标原点，焦点在x轴上，F1，F2分别为左、右焦点，双曲线的左支上有一点P，∠F1PF2＝，且△PF1F2的面积为2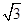，双曲线的离心率为2，求该双曲线的标准方程．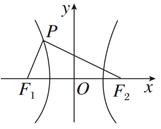
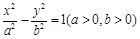已知F1、F2分别为双曲线的左、右焦点，点P为双曲线右支上的一点，满足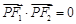，且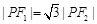，则该双曲线离心率为       ．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网