题目内容
21、已知|
|=2c，|
|=2a（a＞c），2
=
，2
=
，
•
=0（G为动点）（a＞c）．
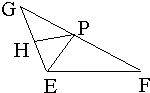
（1）建立适当的平面直角坐标系，求出点P的轨迹方程；
（2）若点P的轨迹上存在两个不同的点A、B，且线段AB的中垂线与EF（或EF的延长线）有唯一的交点C，证明：|
|＜
．
| EF |
| EF |
| EH |
| EG |
| EO |
| EF |
| HP |
| EG |
（1）建立适当的平面直角坐标系，求出点P的轨迹方程；
（2）若点P的轨迹上存在两个不同的点A、B，且线段AB的中垂线与EF（或EF的延长线）有唯一的交点C，证明：|
| OC |
| c2 |
| a |
（1）|PE|+|PF|=|PG|+|PF|=|FG|=2a（＞|EF|），∴点P的轨迹为椭圆
∴轨迹方程为
+
=1
（2）设A（x1，y1），B（x2，y2）．A，B的中点M（x0，y0），C（t，0）．
当kCM不存在时，显然成立．
当kCM存在时，kCM=
．由“点差法”得：kAB=-
•
∵kAB•kCM=-1.x0=
∵|x0|＜a∴|
|＜a∴|t|＜
即|
|＜
．
∴轨迹方程为
| x2 |
| a2 |
| y2 |
| a2-c2 |
（2）设A（x1，y1），B（x2，y2）．A，B的中点M（x0，y0），C（t，0）．
当kCM不存在时，显然成立．
当kCM存在时，kCM=
| y0 |
| x0-t |
| a2-c2 |
| a2 |
| x0 |
| y0 |
∵kAB•kCM=-1.x0=
| a2-t |
| c2 |
| a2-t |
| c2 |
| c2 |
| a |
| OC |
| c2 |
| a |
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
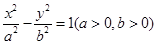的渐近线与圆
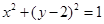相切，则双曲线离心率为（ ）.
的渐近线方程是_________________．
的离心率为2，焦点到渐近线的距离为
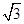，则C的焦距等于( )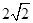
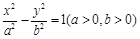右支上的一点，满足
，且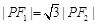
，则该双曲线离心率为 ．