题目内容
【题目】函数![]() ,
,![]() ,其中常数
,其中常数![]() .
.
(1)若函数![]() 与
与![]() 有相同的极值点,求
有相同的极值点,求![]() 的值;
的值;
(2)若![]() ,判断函数
,判断函数![]() 与
与![]() 图象的交点个数.
图象的交点个数.
【答案】(1)![]() ;(2)当
;(2)当![]() 时,有1个交点;当
时,有1个交点;当![]() 时,有3个交点.
时,有3个交点.
【解析】
(1)先求出![]() 的极值点,再通过
的极值点,再通过![]() 与
与![]() 有相同的极值点,可求出
有相同的极值点,可求出![]() 的值;
的值;
(2)判断函数![]() 与
与![]() 图象的交点个数,构造新函数
图象的交点个数,构造新函数![]() ,可将问题转化为求函数
,可将问题转化为求函数![]() 的零点个数,结合a的范围,利用函数的单调性及函数的性质可判断函数的零点存在情况.
的零点个数,结合a的范围,利用函数的单调性及函数的性质可判断函数的零点存在情况.
解:(1)![]() ,
,![]() 的定义域都为
的定义域都为![]() ,
,
![]() ,
,
令![]() ,得
,得![]() ;令
;令![]() ,得
,得![]() ;令
;令![]() ,得
,得![]() ,
,
所以函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
所以函数![]() 在
在![]() 处取得极小值;
处取得极小值;
又![]() .
.
∴![]() ,解得
,解得![]() ,
,
经检验,满足题意,故![]() .
.
(2)函数![]() 与
与![]() 的图象的交点个数等价于函数
的图象的交点个数等价于函数![]() 的零点个数.
的零点个数.
![]() ,则
,则![]() .
.
①当![]() 时,令
时,令![]() ,则
,则![]() .
.
令![]() ,得
,得![]() ,
,
令![]() ,得
,得![]() ,
,
故函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
故![]() .
.
则![]() .故
.故![]() 在
在![]() 上是增函数,此时由
上是增函数,此时由![]() ,可得函数
,可得函数![]() 有唯一的零点.
有唯一的零点.
即函数![]() 与
与![]() 的图象有1个交点;
的图象有1个交点;
②当![]() 时,
时,![]() ,
,
并且对于负数![]() ,有
,有
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
又因为![]() ,
,
所以![]() ,
,
所以![]() .
.
所以在区间![]() 上存在负数
上存在负数![]() ,使得
,使得![]() ,
,
则在![]() 上,
上,![]() ,
,![]() 是增函数,
是增函数,
在区间![]() 上,
上,![]() ,
,![]() 是减函数.
是减函数.
则![]() ,
,![]() .
.
所以在![]() 上,
上,![]() 有且仅有1个零点;
有且仅有1个零点;
在区间![]() 上,
上,![]() ,
,![]() 且
且![]() 是增函数,
是增函数,
所以存在正数![]() ,使得在
,使得在![]() 上,
上,![]() ,
,![]() 是减函数;
是减函数;
在![]() 上,
上,![]() ,
,![]() 是增函数.
是增函数.
于是有![]() ,
,![]() .
.
所以在![]() 上,
上,![]() 恰有唯一的零点
恰有唯一的零点
所以当![]() 时,
时,![]() 在
在![]() 上恰有三个不同的零点.
上恰有三个不同的零点.
即函数![]() 与
与![]() 的图象有3个交点.
的图象有3个交点.
综上所述,当![]() 时,函数
时,函数![]() 与
与![]() 的图象有1个交点;当
的图象有1个交点;当![]() 时,函数
时,函数![]() 与
与![]() 的图象有3个交点.
的图象有3个交点.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】盲盒里面通常装的是动漫、影视作品的周边,或者设计师单独设计出来的玩偶.由于盒子上没有标注,购买者只有打开才会知道自己买到了什么,因此这种惊喜吸引了众多年轻人,形成了“盲盒经济”.某款盲盒内可能装有某一套玩偶的![]() 、
、![]() 、
、![]() 三种样式,且每个盲盒只装一个.
三种样式,且每个盲盒只装一个.
(1)若每个盲盒装有![]() 、
、![]() 、
、![]() 三种样式玩偶的概率相同.某同学已经有了
三种样式玩偶的概率相同.某同学已经有了![]() 样式的玩偶,若他再购买两个这款盲盒,恰好能收集齐这三种样式的概率是多少?
样式的玩偶,若他再购买两个这款盲盒,恰好能收集齐这三种样式的概率是多少?
(2)某销售网点为调查该款盲盒的受欢迎程度,随机发放了200份问卷,并全部收回.经统计,有![]() 的人购买了该款盲盒,在这些购买者当中,女生占
的人购买了该款盲盒,在这些购买者当中,女生占![]() ;而在未购买者当中,男生女生各占
;而在未购买者当中,男生女生各占![]() .请根据以上信息填写下表,并分析是否有
.请根据以上信息填写下表,并分析是否有![]() 的把握认为购买该款盲盒与性别有关?
的把握认为购买该款盲盒与性别有关?
女生 | 男生 | 总计 | |
购买 | |||
未购买 | |||
总计 |
参考公式: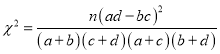 ,其中
,其中![]() .
.
span>参考数据:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(3)该销售网点已经售卖该款盲盒6周,并记录了销售情况,如下表:
周数 | 1 | 2 | 3 | 4 | 5 | 6 |
盒数 | 16 | ______ | 23 | 25 | 26 30 |
由于电脑故障,第二周数据现已丢失,该销售网点负责人决定用第4、5、6周的数据求线性回归方程,再用第1、3周数据进行检验.
①请用4、5、6周的数据求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(注: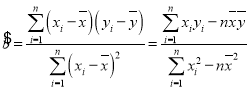 ,
,![]() )
)
②若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2盒,则认为得到的线性回归方程是可靠的,试问①中所得的线性回归方程是否可靠?