题目内容
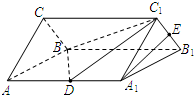 (2009•孝感模拟)如图:D、E分别是正三棱柱ABC-A1B1C1的棱AA1、B1C1的中点,且棱AA1=8,AB=4,
(2009•孝感模拟)如图:D、E分别是正三棱柱ABC-A1B1C1的棱AA1、B1C1的中点,且棱AA1=8,AB=4,(1)求证:A1E∥平面BDC1.
(2)求二面角A1-BC1-B1的大小.
分析:(1)欲证线面平行,关键是证线线平行.在线段BC1上取中点F,连接EF、DF,可得EF∥DA1,且EF=DA1,所以四边形EFDA1是平行四边形,所以A1E∥FD,再结合线面平行的判定定理可得线面平行.
(2)先作出二面角A1-BC1-B1的平面角:A1E⊥B1C1,A1E⊥CC1,得A1E⊥平面CBB1C1,过点E作EH⊥BC1于H,连接A1H,则∠A1HE为二面角A1-BC1-B1的平面角,再分别求出EH,A1E的长,利用正切函数可求.
(2)先作出二面角A1-BC1-B1的平面角:A1E⊥B1C1,A1E⊥CC1,得A1E⊥平面CBB1C1,过点E作EH⊥BC1于H,连接A1H,则∠A1HE为二面角A1-BC1-B1的平面角,再分别求出EH,A1E的长,利用正切函数可求.
解答:证明:在线段BC1上取中点F,连接EF、DF
则由题意得EF∥DA1,且EF=DA1,
∴四边形EFDA1是平行四边形
∴A1E∥FD,又A1E?平面BDC1,FD?平面BDC1
∴A1E∥平面BDC1 …(6分)
(2)由A1E⊥B1C1,A1E⊥CC1,得A1E⊥平面CBB1C1,过点E作
EH⊥BC1于H,连接A1H,则∠A1HE为二面角A1-BC1-B1的平面角 …(8分)
在Rt△BB1C1中,由BB1=8,B1C1=4,得BC1边上的高为
,∴EH=
,
又A1E=2,∴tan∠A1HE=
∴二面角A1-BC1-B1为arctan
…(12分)
则由题意得EF∥DA1,且EF=DA1,
∴四边形EFDA1是平行四边形
∴A1E∥FD,又A1E?平面BDC1,FD?平面BDC1
∴A1E∥平面BDC1 …(6分)
(2)由A1E⊥B1C1,A1E⊥CC1,得A1E⊥平面CBB1C1,过点E作
EH⊥BC1于H,连接A1H,则∠A1HE为二面角A1-BC1-B1的平面角 …(8分)
在Rt△BB1C1中,由BB1=8,B1C1=4,得BC1边上的高为
| 8 |
| 5 |
| 5 |
| 4 |
| 5 |
| 5 |
又A1E=2,∴tan∠A1HE=
| ||
| 2 |
∴二面角A1-BC1-B1为arctan
| ||
| 2 |
点评:本题的考点是与二面角有关的立体几何综合问题.主要考查用线面平行的判定定理证明线面平行,以及求二面角的平面角,而空间角解决的关键是做角,由图形的结构及题设条件正确作出平面角来,是求角的关键.

练习册系列答案
相关题目
 (2009•孝感模拟)设全集U=R,A={x|2x(x+3)<1},B={x|y=ln(-1-x)},则图中阴影部分表示的集合为( )
(2009•孝感模拟)设全集U=R,A={x|2x(x+3)<1},B={x|y=ln(-1-x)},则图中阴影部分表示的集合为( )