题目内容
19.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)过点(1,$\frac{\sqrt{3}}{2}$)且离心率为$\frac{\sqrt{3}}{2}$.(1)求椭圆C的标准方程;
(2)过x轴上一点(m,0)作⊙O:x2+y2=1的切线l,交椭圆C于M、N两点,求|MN|的最大值.
分析 (1)利用已知条件结合隐含条件得到关于a,b的方程组,求出a,b后即可求椭圆C的方程;
(2)利用直线的斜率存在与不存在,分别与椭圆方程联立,利用韦达定理,以及弦长公式表示弦长|MN|通过基本不等式求解弦长的最大值.
解答 解:(1)由题得:$\frac{c}{a}=\frac{\sqrt{3}}{2}$,即$\frac{{a}^{2}-{b}^{2}}{{a}^{2}}=\frac{3}{4}$,
又椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)过点(1,$\frac{\sqrt{3}}{2}$),
∴$\frac{1}{{a}^{2}}+\frac{3}{4{b}^{2}}=1$,解得a2=4,b2=1.
∴椭圆C的方程为$\frac{{x}^{2}}{4}+{y}^{2}=1$;
(2)由题意知,|m|≥1.
当m=1时,切线l的方程x=1,点M、N的坐标分别为(1,$\frac{\sqrt{3}}{2}$),(1,-$\frac{\sqrt{3}}{2}$),
此时|MN|=$\sqrt{3}$;
当m=-1时,同理可得|MN|=$\sqrt{3}$;
当|m|>1时,设切线l的方程为y=k(x-m),(k≠0)
由$\left\{\begin{array}{l}{y=k(x-m)}\\{\frac{{x}^{2}}{4}+{y}^{2}=1}\end{array}\right.$,得(1+4k2)x2-8k2mx+4k2m2-4=0.
设M、N两点的坐标分别为(x1,y1),(x2,y2),
则△=64k4m2-16(1+4k2)(4k2m2-4)=48k2>0.
${x}_{1}+{x}_{2}=\frac{8{k}^{2}m}{1+4{k}^{2}},{x}_{1}{x}_{2}=\frac{4{k}^{2}{m}^{2}-4}{1+4{k}^{2}}$,
又由l与圆x2+y2=1相切,得
$\frac{|km|}{\sqrt{{k}^{2}+1}}=1$,即m2k2=k2+1.得${k}^{2}=\frac{1}{{m}^{2}-1}$.
∴|MN|=$\sqrt{1+{k}^{2}}\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{1+{k}^{2}}\sqrt{(\frac{8{k}^{2}m}{1+4{k}^{2}})^{2}-4•\frac{4{k}^{2}{m}^{2}-4}{1+4{k}^{2}}}$=$\frac{4\sqrt{3}|m|}{{m}^{2}+3}$.
∵|m|≥1,∴|MN|=$\frac{4\sqrt{3}|m|}{{m}^{2}+3}$=$\frac{4\sqrt{3}}{|m|+\frac{3}{|m|}}$≤2,
且当m=±$\sqrt{3}$时,|MN|=2,
由于当m=±1时,|MN|=$\sqrt{3}$,
∴|MN|的最大值为2.
点评 本题考查椭圆的方程的求法,直线与椭圆的位置关系,弦长公式的应用,考查分析问题解决问题的能力以及转化思想的应用,是压轴题.

| A. | $\frac{3}{2}$e${\;}^{\frac{2}{3}}$ | B. | $\frac{13}{6}$e6 | C. | $\frac{1}{6}$e6 | D. | $\frac{7}{2}$e${\;}^{\frac{2}{3}}$ |
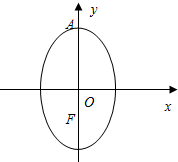 已知动圆Q过定点F(0,-1),且与直线l:y=1相切,椭圆N的对称轴为坐标轴,O点为坐标原点,F是其一个焦点,又点A(0,2)在椭圆N上.
已知动圆Q过定点F(0,-1),且与直线l:y=1相切,椭圆N的对称轴为坐标轴,O点为坐标原点,F是其一个焦点,又点A(0,2)在椭圆N上.