题目内容
【题目】如图,在长方体ABCD﹣A1B1C1D1中AA1=AD=1,E为CD中点.
(Ⅰ)求证:B1E⊥AD1;
(Ⅱ)在棱AA1上是否存在一点P,使得DP∥平面B1AE?若存在,求AP的长;若不存在,说明理由.
(Ⅲ)若二面角A﹣B1E﹣A1的大小为30°,求AB的长.
【答案】解:(I)以A为原点, ![]() ,
, ![]() ,
, ![]() 的方向为X轴,Y轴,Z轴的正方向建立空间直角坐标系,如图,
的方向为X轴,Y轴,Z轴的正方向建立空间直角坐标系,如图,
设AB=a,则A(0,0,0),D(0,1,0),D1(0,1,1),E( ![]() ,1,0),B1(a,0,1)
,1,0),B1(a,0,1)
故 ![]() =(0,1,1),
=(0,1,1), ![]() =(﹣
=(﹣ ![]() ,1,﹣1),
,1,﹣1), ![]() =(a,0,1),
=(a,0,1), ![]() =(
=( ![]() ,1,0),
,1,0),
∵ ![]()
![]() =1﹣1=0
=1﹣1=0
∴B1E⊥AD1;
(II)假设在棱AA1上存在一点P(0,0,t),使得DP∥平面B1AE.此时 ![]() =(0,﹣1,t).
=(0,﹣1,t).
又设平面B1AE的法向量 ![]() =(x,y,z).
=(x,y,z).
∵ ![]() ⊥平面B1AE,∴
⊥平面B1AE,∴ ![]() ⊥B1A,
⊥B1A, ![]() ⊥AE,得
⊥AE,得 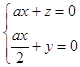 ,取x=1,得平面B1AE的一个法向量
,取x=1,得平面B1AE的一个法向量 ![]() =(1,﹣
=(1,﹣ ![]() ,﹣a).
,﹣a).
要使DP∥平面B1AE,只要 ![]() ⊥
⊥ ![]() ,即有
,即有 ![]()
![]() =0,有此得
=0,有此得 ![]() ﹣at=0,解得t=
﹣at=0,解得t= ![]() ,即P(0,0,
,即P(0,0, ![]() ),
),
又DP平面B1AE,
∴存在点P,满足DP∥平面B1AE,此时AP= ![]()
(III)连接A1D,B1C,由长方体ABCD﹣A1B1C1D1及AA1=AD=1,得AD1⊥A1D.
∵B1C∥A1D,∴AD1⊥B1C.
由(I)知,B1E⊥AD1 , 且B1C∩B1E=B1 .
∴AD1⊥平面DCB1A1 ,
∴ ![]() 是平面B1A1E的一个法向量,此时
是平面B1A1E的一个法向量,此时 ![]() =(0,1,1).
=(0,1,1).
设 ![]() 与
与 ![]() 所成的角为θ,则cosθ=
所成的角为θ,则cosθ= 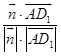 =
= 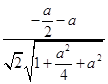
∵二面角A﹣B1E﹣A1的大小为30°,
∴|cosθ|=cos30°= ![]() ,即|
,即| 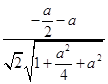 |=
|= ![]() ,解得a=2,即AB的长为2
,解得a=2,即AB的长为2
【解析】(Ⅰ)由题意及所给的图形,可以A为原点, ![]() ,
, ![]() ,
, ![]() 的方向为X轴,Y轴,Z轴的正方向建立空间直角坐标系,设AB=a,给出图形中各点的坐标,可求出向量
的方向为X轴,Y轴,Z轴的正方向建立空间直角坐标系,设AB=a,给出图形中各点的坐标,可求出向量 ![]() 与
与 ![]() 的坐标,验证其数量积为0即可证出两线段垂直.(II)由题意,可先假设在棱AA1上存在一点P(0,0,t),使得DP∥平面B1AE,求出平面B1AE法向量,可法向量与直线DP的方向向量内积为0,由此方程解出t的值,若能解出,则说明存在,若不存在符合条件的t的值,说明不存在这样的点P满足题意.(III)由题设条件,可求面夹二面角的两个平面的法向量,利用两平面的夹角为30°建立关于a的方程,解出a的值即可得出AB的长
的坐标,验证其数量积为0即可证出两线段垂直.(II)由题意,可先假设在棱AA1上存在一点P(0,0,t),使得DP∥平面B1AE,求出平面B1AE法向量,可法向量与直线DP的方向向量内积为0,由此方程解出t的值,若能解出,则说明存在,若不存在符合条件的t的值,说明不存在这样的点P满足题意.(III)由题设条件,可求面夹二面角的两个平面的法向量,利用两平面的夹角为30°建立关于a的方程,解出a的值即可得出AB的长
【考点精析】掌握空间中直线与直线之间的位置关系和直线与平面平行的判定是解答本题的根本,需要知道相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点;平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行.

 阅读快车系列答案
阅读快车系列答案

