题目内容
【题目】已知函数f(x)= ![]() sinxcosx+sin2x+
sinxcosx+sin2x+ ![]() (x∈R).
(x∈R).
(Ⅰ)当x∈[﹣ ![]() ,
, ![]() ]时,求f(x)的最大值.
]时,求f(x)的最大值.
(Ⅱ)设△ABC的内角A,B,C所对的边分别为a,b,c,且c= ![]() ,f(C)=2,sinB=2sinA,求a.
,f(C)=2,sinB=2sinA,求a.
【答案】解:(Ⅰ)函数f(x)= ![]() sinxcosx+sin2x+
sinxcosx+sin2x+ ![]()
= ![]() sin2x+
sin2x+ ![]() +
+ ![]()
= ![]() sin2x﹣
sin2x﹣ ![]() cos2x+1
cos2x+1
=sin(2x﹣ ![]() )+1(x∈R),
)+1(x∈R),
当x∈[﹣ ![]() ,
, ![]() ]时,2x﹣
]时,2x﹣ ![]() ∈[﹣
∈[﹣ ![]() ,
, ![]() ],
],
令2x﹣ ![]() =
= ![]() ,解得x=
,解得x= ![]() ,
,
此时sin(2x﹣ ![]() )=1,
)=1,
f(x)取得最大值f(x)max=2;
(Ⅱ)∵f(C)=sin(2C﹣ ![]() )+1=2,
)+1=2,
∴ ![]() ,
,
∵0<C<π,∴ ![]() ,
,
令 ![]() ,
,
解得 ![]() ;
;
又∵sinB=2sinA,
∴ ![]() ,
,
∴b=2a;由余弦定理得:c2=a2+b2﹣2abcos ![]() =3,
=3,
几a2+b2﹣ab=3,
整理得5a2﹣2a﹣3=0,
解得a=1或a=﹣ ![]() (不合题意,舍去),
(不合题意,舍去),
∴a的值是1.
【解析】(Ⅰ)化简函数f(x)为正弦型函数,根据x∈[﹣ ![]() ,
, ![]() ],求出2x﹣
],求出2x﹣ ![]() 的范围,从而求出f(x)的最大值;(Ⅱ)根据f(C)=2求出C的值,再由正弦、余弦定理,即可求出a的值.
的范围,从而求出f(x)的最大值;(Ⅱ)根据f(C)=2求出C的值,再由正弦、余弦定理,即可求出a的值.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】已知产品![]() 的质量采用综合指标值
的质量采用综合指标值![]() 进行衡量,
进行衡量,![]() 为一等品;
为一等品;![]() 为二等品;
为二等品;![]() 为三等品.我市一家工厂准备购进新型设备以提高生产产品
为三等品.我市一家工厂准备购进新型设备以提高生产产品![]() 的效益,在某供应商提供的设备中任选一个试用,生产了一批产品并统计相关数据,得到频率分布直方图:
的效益,在某供应商提供的设备中任选一个试用,生产了一批产品并统计相关数据,得到频率分布直方图:
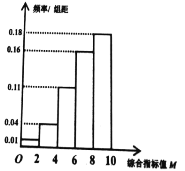
(1)估计该新型设备生产的产品![]() 为二等品的概率;
为二等品的概率;
(2)根据这家工厂的记录,产品各等次的销售率(某等次产品销量与其对应产量的比值)及单件售价情况如下:
一等品 | 二等品 | 三等品 | |
销售率 |
|
|
|
单件售价 |
|
|
|
根据以往的销售方案,未售出的产品统一按原售价的![]() 全部处理完.已知该工厂认购该新型设备的前提条件是,该新型设备生产的产品同时满足下列两个条件:
全部处理完.已知该工厂认购该新型设备的前提条件是,该新型设备生产的产品同时满足下列两个条件:
①综合指标值的平均数不小于![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
②单件平均利润值不低于![]() .
.
若该新型设备生产的产品![]() 的成本为
的成本为![]() 元/件,月产量为
元/件,月产量为![]() 件,在销售方案不变的情况下,根据以上图表数据,分析该新型设备是否达到该工厂的认购条件.
件,在销售方案不变的情况下,根据以上图表数据,分析该新型设备是否达到该工厂的认购条件.


