题目内容
16.求y=$\frac{1}{si{n}^{2}θ}$+$\frac{3}{co{s}^{2}θ}$的最小值.分析 由条件利用同角三角函数的基本关系化简函数的解析式为y=4+cot2θ+3tan2θ,再利用基本不等式求得它的最小值.
解答 解:y=$\frac{1}{si{n}^{2}θ}$+$\frac{3}{co{s}^{2}θ}$=$\frac{{sin}^{2}θ{+cos}^{2}θ}{{sin}^{2}θ}$+$\frac{{3sin}^{2}θ+{3cos}^{2}θ}{{cos}^{2}θ}$=4+cot2θ+3tan2θ≥4+2$\sqrt{3}$,
当且仅当|cotθ|=$\sqrt{3}$|tanθ|时,取等号,故y的最小值为4+2$\sqrt{3}$.
点评 本题主要考查同角三角函数的基本关系,基本不等式的应用,属于基础题.

练习册系列答案
 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
6.若函数f(x)的定义域是(0,2),则f(3-3x)的定义域是( )
| A. | (0,2) | B. | (-2,0) | C. | (0,1) | D. | (-1,0) |
1.函数y=$\frac{{x}^{2}+2x+6}{x-1}$(x>1)的最小值为( )
| A. | 10 | B. | 9 | C. | 6 | D. | 4 |
8.${∫}_{-\frac{π}{2}}^{\frac{π}{2}}$(cos$\frac{x}{2}$-sin$\frac{x}{2}$)2dx=( )
| A. | $\frac{π}{2}$ | B. | π | C. | $\frac{3π}{2}$ | D. | 2π |
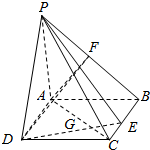 如图,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,AB=PA=1,AD=$\sqrt{3}$,E、F、G分别是BC、PB、AD上的点,且AF⊥PC,AG=3GD.
如图,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,AB=PA=1,AD=$\sqrt{3}$,E、F、G分别是BC、PB、AD上的点,且AF⊥PC,AG=3GD.