题目内容
13.化简3$C_{10}^1+9C_{10}^2+…+{3^{10}}C_{10}^{10}$=410-1(用数式表示).分析 根据二项式定理的公式,逆用公式即可化简.
解答 解:3$C_{10}^1+9C_{10}^2+…+{3^{10}}C_{10}^{10}$
=${C}_{10}^{0}$+${C}_{10}^{1}$•3+${C}_{10}^{2}$•32+…+${C}_{10}^{10}$•310-${C}_{10}^{0}$
=(1+3)10-1
=410-1.
故答案为:410-1.
点评 本题考查了二项式定理的应用问题,也考查了公式的逆用问题,是基础题目.

练习册系列答案
相关题目
8.延迟退休年龄的问题,近期引发社会的关注. 人社部于2012年7月25日上午召开新闻发布会表示,我国延迟退休年龄将借鉴国外经验,拟对不同群体采取差别措施,并以“小步慢走”的方式实施.推迟退休年龄似乎是一种必然趋势,然而反对的声音也随之而起.现对某市工薪阶层关于“延迟退休年龄”的态度进行调查,随机抽取了50人,他们月收入的频数分布及对“延迟退休年龄”反对的人数
根据已知条件完成下面的2×2列联表,问能否在犯错误的概率不超过0.01的前提下认为月收入以5000为分界点的“延迟退休年龄”的态度有差异?
附:临界值表
参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d.
| 月收入(元) | [1000,2000) | [2000,3000) | [3000,4000) | [4000,5000) | [5000,6000) | [6000,7000) |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 反对人数 | 4 | 8 | 12 | 5 | 2 | 1 |
| 月收入不低于5000元的人数 | 月收入低于5000元的人数 | 总计 | |
| 反对 | |||
| 赞成 | |||
| 总计 |
| P(k2≥k0) | 0.05 | 0.025 | 0.010 | 0.005 |
| k0 | 3.841 | 5.024 | 6.635 | 7.879 |
18.下列函数是奇函数的是( )
| A. | f(x)=x|x| | B. | f(x)=lgx | C. | f(x)=2x+2-x | D. | f(x)=x3-1 |
 .
.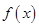 最小正周期;
最小正周期;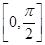 上的最大值和最小值.
上的最大值和最小值. ,则集合
,则集合 ___________.
___________.