题目内容
函数y=(acosx+bsinx)cosx有最大值2,最小值-1,则实数(ab)2的值为________.
8
y=acos2x+bsinxcosx
=a·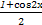 +
+ sin 2x
sin 2x
=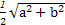 sin(2x+φ)+
sin(2x+φ)+ ,
,
∴
∴a=1,b2=8,∴(ab)2=8.
【方法技巧】三角恒等变换的特点
(1)三角恒等变换就是利用两角和与差的正弦、余弦、正切公式、倍角公式、半角公式等进行简单的恒等变换.三角恒等变换位于三角函数与数学变换的结合点上.
(2)对于三角变换,由于不同的三角函数式不仅会有结构形式方面的差异,而且还会有所包含的角,以及这些角的三角函数种类方面的差异,因此三角恒等变换常常首先寻找式子所包含的各个角之间的联系,这是三角恒等变换的重要特点.
=a·
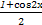 +
+ sin 2x
sin 2x=
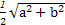 sin(2x+φ)+
sin(2x+φ)+ ,
,∴

∴a=1,b2=8,∴(ab)2=8.
【方法技巧】三角恒等变换的特点
(1)三角恒等变换就是利用两角和与差的正弦、余弦、正切公式、倍角公式、半角公式等进行简单的恒等变换.三角恒等变换位于三角函数与数学变换的结合点上.
(2)对于三角变换,由于不同的三角函数式不仅会有结构形式方面的差异,而且还会有所包含的角,以及这些角的三角函数种类方面的差异,因此三角恒等变换常常首先寻找式子所包含的各个角之间的联系,这是三角恒等变换的重要特点.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
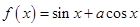 的图象经过点
的图象经过点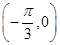 .
.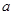 的值;
的值;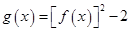 ,求函数
,求函数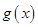 的最小正周期与单调递增区间.
的最小正周期与单调递增区间.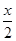 cos
cos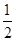
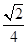 ,α∈(0,π),求α的值;
,α∈(0,π),求α的值;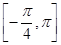 上最大值和最小值.
上最大值和最小值.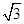 cos x,cos x),b=(sin x,2cos x),设函数f(x)=a·b+|b|2+
cos x,cos x),b=(sin x,2cos x),设函数f(x)=a·b+|b|2+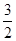 .
.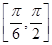 时,求函数f(x)的值域;
时,求函数f(x)的值域;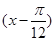 的值;
的值;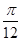 个单位后,再将得到的图象上各点的纵坐标向下平移5个单位,得到函数y=g(x)的图象,求函数g(x)的表达式并判断奇偶性.
个单位后,再将得到的图象上各点的纵坐标向下平移5个单位,得到函数y=g(x)的图象,求函数g(x)的表达式并判断奇偶性.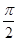 时,取最大值A,在x=
时,取最大值A,在x=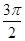 时,取最小值-A,则当x=π时,函数y的值( )
时,取最小值-A,则当x=π时,函数y的值( ) sin2x-
sin2x- -
- .
. ,
, ],求函数f(x)的最值及对应的x的值.
],求函数f(x)的最值及对应的x的值. )的图象经过点(0,1),且
)的图象经过点(0,1),且 一个最高点的坐标为(1,2),则ω的最小值是 .
一个最高点的坐标为(1,2),则ω的最小值是 . )在[0,
)在[0, ]上的最大值为M,最小值为m,则M+m等于( )
]上的最大值为M,最小值为m,则M+m等于( )

 个单位长度,再把所得各点的横坐标伸长到原来的2倍(纵坐标不变),则所得函数图象的解析式是________.
个单位长度,再把所得各点的横坐标伸长到原来的2倍(纵坐标不变),则所得函数图象的解析式是________.