题目内容
【题目】已知点(1, ![]() )是函数f(x)=
)是函数f(x)= ![]() ax(a>0,a≠1)图象上一点,等比数列{an}的前n项和为c﹣f(n).数列{bn}(bn>0)的首项为2c,前n项和满足
ax(a>0,a≠1)图象上一点,等比数列{an}的前n项和为c﹣f(n).数列{bn}(bn>0)的首项为2c,前n项和满足 ![]() =
= ![]() +1(n≥2). (Ⅰ)求数列{an}的通项公式;
+1(n≥2). (Ⅰ)求数列{an}的通项公式;
(Ⅱ)若数列{ ![]() }的前n项和为Tn , 问使Tn>
}的前n项和为Tn , 问使Tn> ![]() 的最小正整数n是多少?
的最小正整数n是多少?
【答案】(Ⅰ)解: ![]() .∴
.∴ ![]() , ∵
, ∵ ![]() ,则等比数列{an}的前n项和为c﹣
,则等比数列{an}的前n项和为c﹣ ![]()
![]() ,a2=(c﹣
,a2=(c﹣ ![]() )﹣(c﹣
)﹣(c﹣ ![]() )=
)= ![]() ,
, ![]()
由{an}为等比数列,得公比q= ![]()
∴ 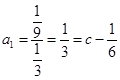 ,则c=
,则c= ![]() ,a
,a ![]()
∴ ![]()
(Ⅱ):由b1=2c=1,得s1=1
n≥2时, ![]() ,则
,则 ![]() 是首项为1,公差为1的等差数列.
是首项为1,公差为1的等差数列.
∴ ![]() ,
, ![]() (n∈N+)
(n∈N+)
则 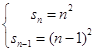 (n≥2)bn=2n﹣1,(n≥2).
(n≥2)bn=2n﹣1,(n≥2).
当n=1时,b1=1满足上式
∴ ![]()
∵ ![]() =
= ![]() =
= ![]()
∴Tn= ![]() =
= ![]() =
= ![]()
由Tn= ![]() ,得n
,得n ![]() ,则最小正整数n为59
,则最小正整数n为59
【解析】(Ⅰ)由已知求得a, ![]() ,a2=(c﹣
,a2=(c﹣ ![]() )﹣(c﹣
)﹣(c﹣ ![]() )=
)= ![]() ,
, ![]() ,得公比q=
,得公比q= ![]() ,即可写出通项;(Ⅱ)可得
,即可写出通项;(Ⅱ)可得 ![]() 是首项为1,公差为1的等差数列.由
是首项为1,公差为1的等差数列.由 ![]() (n≥2)bn=2n﹣1,(n≥2).
(n≥2)bn=2n﹣1,(n≥2). ![]() =
= ![]() =
= ![]() ,累加求得Tn=
,累加求得Tn= ![]() ,得n
,得n ![]() ,即可得最小正整数n.
,即可得最小正整数n.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目