Question

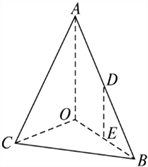
【题目】如图，直四棱柱中，四边形为梯形， ，且.过三点的平面记为， 与的交点为.

(I)证明： 为的中点；

(II)求此四棱柱被平面所分成上下两部分的体积之比.

Answer 1

【答案】(1)见解析;(2) .

【解析】试题分析：（1）由已知得平面QBC∥平面A1AD，从而QC∥A1D，由此能证明Q为BB1的中点．

（2）连接QA，QD．设AA1=h，梯形ABCD的高为d，四棱柱被平面α所分成上下两部分的体积分别为V上和V下，BC=a，则AD=2a．V下=+V四棱锥QABCD=ahd .

= ahd，由此能求出此四棱柱被平面α所分成上下两部分的体积之比．

(I)证明：延长交于，则平面，

又平面，平面平面，

所以因为

所以，即为的中点．

(II)如图所示，连接.设，梯形的高为，四棱柱被平面所分成上下两部分的体积分别为和， ，则 .

三棱椎， 四棱椎 所以＝三棱椎+四棱椎= .又四棱柱，

所以＝四棱柱－，

故.