题目内容
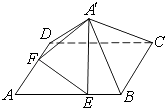
【题目】用5种不同的颜色给如图中所给出的四个区域涂色,每个区域涂一种颜色,若要求相邻(有公共边)的区域不同色,那么共有种不同的涂色方法. 
【答案】260
【解析】解:对于1号区域,有5种颜色可选,即有5种涂法, 分类讨论其他3个区域:①若2、3号区域涂不同的颜色,则有A42=12种涂法,4号区域有3种涂法,此时其他3个区域有12×3=36种涂法;
②若2、3号区域涂相同的颜色,则有4种涂法,4号区域有4种涂法,此时其他3个区域有有4×4=16种涂法;
则共有5×(36+16)=5×52=260种;
故答案为:260.
根据题意,先分析于1号区域,有5种颜色可选,即有5种涂法方案,再分①若2、3号区域涂不同的颜色,②若2、3号区域涂相同的颜色,两种情况讨论其他3个区域的涂色方案,由分类计数原理可得其他个区域的涂色方案的数目;再由分步计数原理计算可得答案.

练习册系列答案
相关题目