题目内容
【题目】如图所示,已知长方体ABCD﹣A1B1C1D1中,AB=BC=2,AA1=4,E是棱CC1上的点,且BE⊥B1C. 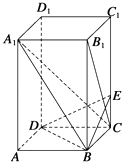
(1)求CE的长;
(2)求证:A1C⊥平面BED;
(3)求A1B与平面BDE夹角的正弦值.
【答案】
(1)解:如图所示,以D为原点,DA、DC、DD1所在直线分别为x、y、z轴建立空间直角坐标系D﹣xyz.
∴D(0,0,0),A(2,0,0),B(2,2,0),C(0,2,0),A1(2,0,4),
B1(2,2,4),C1(0,2,4),D1(0,0,4).
设E点坐标为(0,2,t),则 ![]() =(﹣2,0,t),
=(﹣2,0,t), ![]() =(﹣2,0,﹣4).
=(﹣2,0,﹣4).
∵BE⊥B1C,∴ ![]()
![]() =4+0﹣4t=0.
=4+0﹣4t=0.
∴t=1,故CE=1.
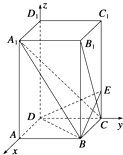
(2)证明:由(1)得,E(0,2,1), ![]() =(﹣2,0,1),
=(﹣2,0,1),
又 ![]() =(﹣2,2,﹣4),
=(﹣2,2,﹣4), ![]() =(2,2,0)
=(2,2,0)
∴ ![]()
![]() =4+0﹣4=0,且
=4+0﹣4=0,且 ![]()
![]() =﹣4+4+0=0.
=﹣4+4+0=0.
∴ ![]() ⊥
⊥ ![]() 且
且 ![]() ⊥
⊥ ![]() ,即A1C⊥DB,A1C⊥BE,
,即A1C⊥DB,A1C⊥BE,
又∵DB∩BE=B,∴A1C⊥平面BDE,即A1C⊥平面BED
(3)解:由(2)知 ![]() =(﹣2,2,﹣4)是平面BDE的一个法向量.
=(﹣2,2,﹣4)是平面BDE的一个法向量.
又 ![]() =(0,2,﹣4),
=(0,2,﹣4),
∴cos< ![]() ,
, ![]() >=
>= 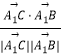 =
= ![]() .
.
∴A1B与平面BDE夹角的正弦值为 ![]()
【解析】(1)建立空间直角坐标系,求出 ![]() 、
、 ![]() ,利用
,利用 ![]()
![]() =0,即可求得结论;(2)证明
=0,即可求得结论;(2)证明 ![]() ⊥
⊥ ![]() 且
且 ![]() ⊥
⊥ ![]() ,可得A1C⊥DB,A1C⊥BE,从而可得A1C⊥平面BED;(3)由(2)知
,可得A1C⊥DB,A1C⊥BE,从而可得A1C⊥平面BED;(3)由(2)知 ![]() =(﹣2,2,﹣4)是平面BDE的一个法向量,利用向量的夹角公式,即可求A1B与平面BDE夹角的正弦值.
=(﹣2,2,﹣4)是平面BDE的一个法向量,利用向量的夹角公式,即可求A1B与平面BDE夹角的正弦值.

 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案【题目】某品牌汽车4s店对最近100位采用分期付款的购车者进行统计,统计结果如表所示:
付款方式 | 分1期 | 分2期 | 分3期 | 分4期 | 分5期 |
频数 | 40 | 20 | a | 10 | b |
已知分3期付款的频率为0.2,4s店经销一辆该品牌的汽车,顾客分1期付款,其利润为1万元,分2期或3期付款其利润为1.5万元,分4期或5期付款,其利润为2万元,用Y表示经销一辆汽车的利润.
(1)求上表中a,b的值.
(2)若以频率作为概率,求事件A:“购买该品牌汽车的3位顾客中,至多有一位采用3期付款”的概率P(A)
(3)求Y的分布列及数学期望EY.