题目内容
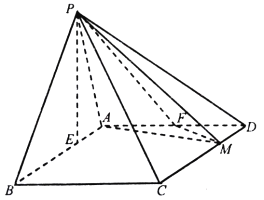
【题目】如图,四边形ABCD中,AB⊥AD,AD∥BC,AD=8,BC=6,AB=2,E,F分别在BC,AD上,EF∥AB,现将四边形ABEF沿EF折起,使得平面ABEF⊥平面EFDC. 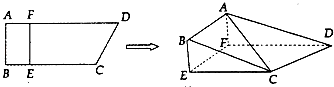
(1)若BE=3,求几何体BEC﹣AFD的体积;
(2)求三棱锥A﹣CDF的体积的最大值,并求此时二面角A﹣CD﹣E的正切值.
【答案】
(1)解:∵平面ABEF⊥平面EFDC,平面ABEF∩平面EFDC=EF,FD⊥EF,
∴FD⊥平面ABEF,又AF平面ABEF,
∴FD⊥AF,又AF⊥EF,FD∩EF=F,
∴AF⊥平面EFDC,
同理,CE⊥平面ABEF,
连结FC,将几何体BEC﹣AFD分成三棱锥A﹣CDF和四棱锥C﹣ABEF,
对于三棱锥A﹣CDF,棱锥高为AF=BE=3,FD=5,
∴V三棱锥A﹣CDF= ![]() =
= ![]() =5,
=5,
对于四棱锥C﹣ABEF,棱锥高为CE=3,
∴V四棱锥C﹣ABEF= ![]() =
= ![]() =6,
=6,
∴几何体BEC﹣AFD的体积V=V三棱锥A﹣CDF+V四棱锥C﹣ABEF=5+6=11
(2)解:设BE=x,∴AF=x(0<x≤6),FD=8﹣x,
∴V三棱锥A﹣CDF= ![]() ,
,
∴当x=4时,V三棱锥A﹣CDF有最大值,且最大值为 ![]() ,
,
在直角梯形CDEF中,EF=2,CE=2,DF=4,
∴CF=2 ![]() ,CD=2
,CD=2 ![]() ,DF=4,
,DF=4,
∴CF2+CD2=DF2,∠DCF=90°,∴DC⊥CF,
又AF⊥平面EFDC,DC平面EFDC,
∴DC⊥AF,又AF∩CF=F,∴DC⊥平面ACF,∴DC⊥AC,
∴∠ACF为二面角A﹣CD﹣E的平面角,
tan ![]() =
= ![]() =
= ![]() ,
,
∴二面角A﹣CD﹣E的正切值为 ![]() .
.
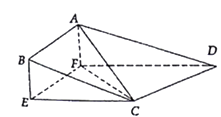
【解析】(1)推导出FD⊥平面ABEF,从而AF⊥平面EFDC,CE⊥平面ABEF,连结FC,将几何体BEC﹣AFD分成三棱锥A﹣CDF和四棱锥C﹣ABEF,由此能求出几何体BEC﹣AFD的体积.(2)设BE=x,则AF=x(0<x≤6),FD=8﹣x,V三棱锥A﹣CDF= ![]() ,当x=4时,V三棱锥A﹣CDF有最大值,∠ACF为二面角A﹣CD﹣E的平面角,由此能求出二面角A﹣CD﹣E的正切值.
,当x=4时,V三棱锥A﹣CDF有最大值,∠ACF为二面角A﹣CD﹣E的平面角,由此能求出二面角A﹣CD﹣E的正切值.

 名校课堂系列答案
名校课堂系列答案