Question

【题目】一个多面体的直观图和三视图如图，M是A1B的中点，N是棱B1C1上的任意一点（含顶点）．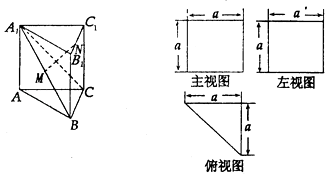

①当点N是棱B1C1的中点时，MN∥平面ACC1A1；
②MN⊥A1C；
③三棱锥N﹣A1BC的体积为VN﹣A BC= a3；
④点M是该多面体外接球的球心．
其中正确的是 ．

Answer 1

【答案】①②③④
【解析】解：①M连接AB中点E，N连接BC中点F，得到MNFE平行于平面ACC1A1 ， 面面平行线面平行，①正确；②M连接A1C中点G，连接C1G，A1C⊥平面MNC1G．∴MN⊥A1C；②正确；③三棱锥N﹣A1BC的体积为VN﹣A= = = a3 ， ③正确；④由三视图可知：此多面体是正方体切割下来了的，M是A1B的中点（空间对角线中点），是正方体中心，∴点M是该多面体外接球的球心．故④正确．
所以答案是：①②③④．
【考点精析】掌握棱柱的结构特征是解答本题的根本，需要知道两底面是对应边平行的全等多边形；侧面、对角面都是平行四边形；侧棱平行且相等；平行于底面的截面是与底面全等的多边形．