题目内容
【题目】某商场营销人员进行某商品![]() 市场营销调查发现,每回馈消费者一定的点数,该商品当天的销量就会发生一定的变化,经过试点统计得到以下表:
市场营销调查发现,每回馈消费者一定的点数,该商品当天的销量就会发生一定的变化,经过试点统计得到以下表:
反馈点数 | 1 | 2 | 3 | 4 | 5 |
销量(百件)/天 | 0.5 | 0.6 | 1 | 1.4 | 1.7 |
(1)经分析发现,可用线性回归模型拟合当地该商品一天销量![]() (百件)与该天返还点数
(百件)与该天返还点数![]() 之间的相关关系.请用最小二乘法求
之间的相关关系.请用最小二乘法求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并预测若返回6个点时该商品当天销量;
,并预测若返回6个点时该商品当天销量;
(2)若节日期间营销部对商品进行新一轮调整.已知某地拟购买该商品的消费群体十分庞大,经过营销部调研机构对其中的200名消费者的返点数额的心理预期值进行了一个抽样调查,得到如下一份频数表:
返还点数预期值区间(百分比) |
|
|
|
|
| |
频数 | 20 | 60 | 60 | 30 | 20 | 10 |
将对返还点数的心理预期值在![]() 和
和![]() 的消费者分别定义为“欲望紧缩型”消费者和“欲望膨胀型”消费者,现采用分层抽样的方法从位于这两个区间的30名消费者中随机抽取6名,再从这6人中随机抽取3名进行跟踪调查,求抽出的3人中至少有1名“欲望膨胀型”消费者的概率.(参考公式及数据:①回归方程
的消费者分别定义为“欲望紧缩型”消费者和“欲望膨胀型”消费者,现采用分层抽样的方法从位于这两个区间的30名消费者中随机抽取6名,再从这6人中随机抽取3名进行跟踪调查,求抽出的3人中至少有1名“欲望膨胀型”消费者的概率.(参考公式及数据:①回归方程![]() ,其中
,其中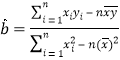 ,
,![]() ;②
;②![]() .)
.)
【答案】(1)![]() ,返回6个点时该商品每天销量约为2百件;(2)(i)
,返回6个点时该商品每天销量约为2百件;(2)(i)![]() ,中位数的估计值为
,中位数的估计值为![]() ,(ii)见解析
,(ii)见解析
【解析】
(1)求出变量![]() 的平均数,求出最小二乘法所需要的数据,可得线性回归方程的系数
的平均数,求出最小二乘法所需要的数据,可得线性回归方程的系数![]() ,再根据样本中心点一定在线性回归方程上,求出
,再根据样本中心点一定在线性回归方程上,求出![]() 的值,写出线性回归方程;
的值,写出线性回归方程; ![]() 代入线性回归方程求出对应的
代入线性回归方程求出对应的![]() 的值,即可预测返回6个点时该商品每天销量;(2)利用分层抽样方法求得“欲望膨胀型”消费者与 “欲望紧缩型”消费者中抽取的人数,利用列举法得到所有的抽样情况共20种,其中至少有1名“欲望膨胀型”消费者的情况有16种,利用古典概型概率公式可得结果.
的值,即可预测返回6个点时该商品每天销量;(2)利用分层抽样方法求得“欲望膨胀型”消费者与 “欲望紧缩型”消费者中抽取的人数,利用列举法得到所有的抽样情况共20种,其中至少有1名“欲望膨胀型”消费者的情况有16种,利用古典概型概率公式可得结果.
(1)易知![]() ,
,
![]() ,
, ,
,
![]() ,
,
则y关于x的线性回归方程为![]() ,
,
当![]() 时,
时,![]() ,即返回6个点时该商品每天销量约为2百件.
,即返回6个点时该商品每天销量约为2百件.
(2)设从“欲望膨胀型”消费者中抽取![]() 人,从“欲望紧缩型”消费者中抽取
人,从“欲望紧缩型”消费者中抽取![]() 人,
人,
由分层抽样的定义可知![]() ,解得
,解得![]() ,
,
在抽取的6人中,2名“欲望膨胀型”消费者分别记为![]() ,4名“欲望紧缩型”消费者分别记为
,4名“欲望紧缩型”消费者分别记为![]() ,则所有的抽样情况如下:
,则所有的抽样情况如下:
![]()
![]()
![]() 共20种,其中至少有1名“欲望膨胀型”消费者的情况有16种,记事件A为“抽出的3人中至少有1名‘欲望膨胀型’消费者”,则
共20种,其中至少有1名“欲望膨胀型”消费者的情况有16种,记事件A为“抽出的3人中至少有1名‘欲望膨胀型’消费者”,则![]() .
.

 阅读快车系列答案
阅读快车系列答案