Question

10．正方形ABCD的边长为2，E是线段CD的中点，F是线段BE上的动点，则$\overrightarrow{BF}$•$\overrightarrow{FC}$的取值范围为[-1，$\frac{4}{5}$]．

Answer 1

分析 以AB为y轴、BC为x轴建立直角坐标系，由题意求出B、C、E的坐标，求出直线BC的方程，设F（x，$\frac{1}{2}x$）（0≤x≤2），由向量的坐标运算求出$\overrightarrow{BF}$、$\overrightarrow{FC}$的坐标，由向量的数量积坐标运算求出$\overrightarrow{BF}•\overrightarrow{FC}$的表达式，利用二次函数的性质求出$\overrightarrow{BF}•\overrightarrow{FC}$的最值和值域．

解答 解：如图：以AB为y轴，BC为x轴建立直角坐标系，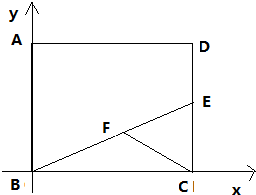
因为正方形ABCD的边长为2，E是线段CD的中点，
所以B（0，0），C（2，0），E（2，1），
则直线BC的方程是y=$\frac{1}{2}x$，
设F（x，$\frac{1}{2}x$）（0≤x≤2），则$\overrightarrow{BF}$=（x，$\frac{1}{2}x$），$\overrightarrow{FC}$=（2-x，-$\frac{1}{2}x$），
所以$\overrightarrow{BF}•\overrightarrow{FC}$=x（2-x）$-\frac{1}{4}{x}^{2}$=$-\frac{5}{4}{x}^{2}+2x$（0≤x≤2），
因为函数y=$-\frac{5}{4}{x}^{2}+2x$的对称轴x=$\frac{4}{5}$，
所以当x=$\frac{4}{5}$时，函数y=$-\frac{5}{4}{x}^{2}+2x$取到最大值是$\frac{4}{5}$，
当x=2时，函数y=$-\frac{5}{4}{x}^{2}+2x$取到最小值是-1，
所以$\overrightarrow{BF}•\overrightarrow{FC}$的取值范围是[-1，$\frac{4}{5}$]，
故答案为：[-1，$\frac{4}{5}$]．

点评 本题考查向量的数量积坐标运算，向量的坐标运算，以及二次函数的性质，属于中档题．