题目内容
1.在同一坐标系中,将曲线4x2+9y2=36变为曲线x′2+y′2=1的伸缩变换是$\left\{\begin{array}{l}{x′=\frac{x}{3}}\\{y′=\frac{y}{2}}\end{array}\right.$.分析 曲线4x2+9y2=36可化为$(\frac{x}{3})^{2}+(\frac{y}{2})^{2}=1$,利用将曲线4x2+9y2=36变为曲线x′2+y′2=1,即可得出结论.
解答 解:曲线4x2+9y2=36可化为$(\frac{x}{3})^{2}+(\frac{y}{2})^{2}=1$,
∵将曲线4x2+9y2=36变为曲线x′2+y′2=1,
∴$\left\{\begin{array}{l}{x′=\frac{x}{3}}\\{y′=\frac{y}{2}}\end{array}\right.$,
故答案为:$\left\{\begin{array}{l}{x′=\frac{x}{3}}\\{y′=\frac{y}{2}}\end{array}\right.$.
点评 本题考查函数的图象变换,曲线4x2+9y2=36化为$(\frac{x}{3})^{2}+(\frac{y}{2})^{2}=1$,是解题的关键.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案
相关题目
12.当n=3时,执行如图所示的程序框图,输出的S值为( )
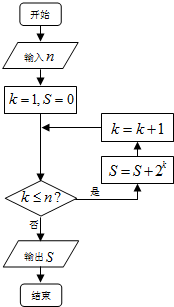

| A. | 30 | B. | 14 | C. | 8 | D. | 6 |
9.阅读如图的程序框图,运行相应的程序则输出的K和S值分别为( )
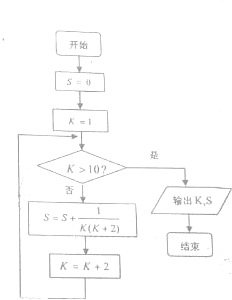

| A. | 9,$\frac{4}{9}$ | B. | 11,$\frac{5}{11}$ | C. | 13,$\frac{6}{13}$ | D. | 15,$\frac{7}{15}$ |
13.若函数f(x)=x3+2x2+mx+1在(-∞,+∞)内单调递增,则m的取值范围是( )
| A. | m≤$\frac{4}{3}$ | B. | m<$\frac{4}{3}$ | C. | m≥$\frac{4}{3}$ | D. | m>$\frac{4}{3}$ |
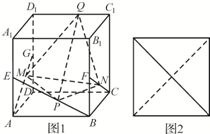 如图1,已知点E、F、G分别是棱长为a的正方体ABCD-A1 B1ClD1的棱AA1、BB1、DD1的中点,点M、N、P、Q分别在线段AG、CF、BE、C1D1上运动,当以M、N、P、Q为顶点的三棱锥Q-PMN的俯视图是如图2所示的正方形时,则点Q到PMN的距离为a.
如图1,已知点E、F、G分别是棱长为a的正方体ABCD-A1 B1ClD1的棱AA1、BB1、DD1的中点,点M、N、P、Q分别在线段AG、CF、BE、C1D1上运动,当以M、N、P、Q为顶点的三棱锥Q-PMN的俯视图是如图2所示的正方形时,则点Q到PMN的距离为a.