题目内容
2.已知数列{an}的前n项和为Sn,点(n,$\frac{{S}_{n}}{n}$)在直线y=$\frac{1}{2}$x+$\frac{11}{2}$上(1)求数列{an}的通项公式;
(2)bn=2${\;}^{{a}_{n}}$,求证:{bn}是等比数列.
分析 (1)求数列{an}的通项公式;
(2)bn=2${\;}^{{a}_{n}}$,求证:{bn}是等比数列.
解答 解:(1)∵点(n,$\frac{{S}_{n}}{n}$)在直线y=$\frac{1}{2}$x+$\frac{11}{2}$上,
∴$\frac{{S}_{n}}{n}$═$\frac{1}{2}$n+$\frac{11}{2}$,
即Sn=$\frac{1}{2}$n2+$\frac{11}{2}$n,
则当n≥2时,an=Sn-Sn-1=$\frac{1}{2}$n2+$\frac{11}{2}$n-[$\frac{1}{2}$(n-1)2+$\frac{11}{2}$(n-1)]=n+5,
即数列{an}的通项公式an=n+5;
证明:(2)∵bn=2${\;}^{{a}_{n}}$,
∴当n≥2时,$\frac{{b}_{n}}{{b}_{n-1}}$=$\frac{{2}^{{a}_{n}}}{{2}^{{a}_{n-1}}}={2}^{{a}_{n}-{a}_{n-1}}={2}^{1}=2$为常数,
故{bn}是等比数列.
点评 本题主要考查等差数列和等比数列的判断,利用数列的递推公式是解决本题的关键.

练习册系列答案
相关题目
12.当n=3时,执行如图所示的程序框图,输出的S值为( )
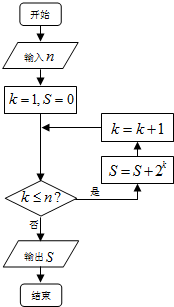

| A. | 30 | B. | 14 | C. | 8 | D. | 6 |
14.下列函数中,最小正周期为π,且图象关于直线x=$\frac{π}{8}$对称的是( )
| A. | y=sin(2x-$\frac{π}{4}$) | B. | y=sin(2x+$\frac{π}{4}$) | C. | y=sin(x+$\frac{π}{8}$) | D. | y=sin(x-$\frac{π}{8}$) |
13.若函数f(x)=x3+2x2+mx+1在(-∞,+∞)内单调递增,则m的取值范围是( )
| A. | m≤$\frac{4}{3}$ | B. | m<$\frac{4}{3}$ | C. | m≥$\frac{4}{3}$ | D. | m>$\frac{4}{3}$ |