题目内容
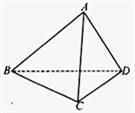在三棱锥A-BCD中，已知侧面ABD⊥底面BCD，若∠ABC=60°，∠CBD=45°，则侧棱AB与底面BCD所成的角为（ ）| A、30° | B、45° | C、60° | D、75° |
分析：利用三面角公式，求出侧棱AB与底面BCD所成的角即可．
解答：解：由题意在三棱锥A-BCD中，已知侧面ABD⊥底面BCD，侧棱AB在底面BCD上的射影为DB，由三面角公式可得：
cos60°=cos45°cos∠ABD．
所以cos∠ABD=
．
∠ABD=45°
故选B．
在三棱锥A-BCD中，已知侧面ABD⊥底面BCD，侧棱AB在底面BCD上的射影为DB，由三面角公式可得：cos60°=cos45°cos∠ABD．
所以cos∠ABD=
| ||
| 2 |
∠ABD=45°
故选B．
点评：本题是基础题，考查直线与平面所成角的求法，考查空间想象能力，计算能力，熟练掌握基本定理、基本方法是解决本题的关键．
练习册系列答案
新课标同步训练系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
如图，在三棱锥A-BCD中，DA，DB，DC两两垂直，且长度均为1，E为BC中点，则下列结论正确的是（ ）
在三棱锥A-BCD中，AB=4，CD=2，且异面直线AB、CD所成的角为60°，若M、N分别是AD、BC的中点，则MN=
（2011•渭南三模）在三棱锥A-BCD中，BD=BC=1，BD⊥BC，DE⊥AB，AD=2，AD⊥平面BCD．
如图所示，在三棱锥A-BCD中，侧面ABD、ACD是全等的直角三角形，AD是公共的斜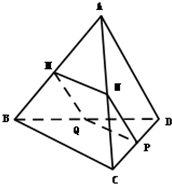
如图，在三棱锥A-BCD中，平行于BC的平面MNPQ分别交AB、AC、CD、BD于M、N、P、Q四点，且MN=PQ．