题目内容
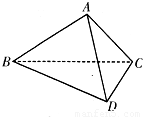
 如图所示,在三棱锥A-BCD中,侧面ABD、ACD是全等的直角三角形,AD是公共的斜
如图所示,在三棱锥A-BCD中,侧面ABD、ACD是全等的直角三角形,AD是公共的斜边,且AD=
| 3 |
(1)当正视图方向与向量
| CD |
(2)求二面角B-AC-D的余弦值;
(3)在线段AC上是否存在一点E,使ED与平面BCD成30°角?若存在,确定点E的位置;若不存在,说明理由.
分析:(1)在Rt△ABD中,AB=
=
,可得BD⊥CD.如图所示,以BD,DC为邻边作正方形CDBP.连接DP交AC于点O.连接AO.可证明CB⊥平面ADP.过点A作AF⊥OD,则AF⊥平面CDBP.进而证明点F与点P重合.据此可得:三棱锥A-BCD的三视图如右图所示.
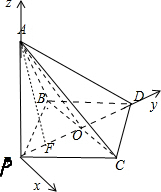
(2)建立如图所示的空间直角坐标系.则P(0,0,0),A(0,0,1),B(-
,
,0),C(
,
,0),D(0,
,0).设平面ABC的法向量为
=(x,y,z),利用
,可得
.同理可求得平面ACD的一个法向量为
.利用cos<
,
>=
即可得到二面角B-AC-D的余弦值.
(3)假设在线段AC上存在一点E,使ED与平面BCD成30°角.设
=λ
,(0≤λ≤1),取平面BCD的法向量为
=(0,0,1).利用sin30°=|cos<
,
>|=
,解得λ即可.
| AD2-BD2 |
| 2 |
(2)建立如图所示的空间直角坐标系.则P(0,0,0),A(0,0,1),B(-
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| 2 |
| n1 |
|
| n1 |
| n2 |
| n1 |
| n2 |
| ||||
|
|
(3)假设在线段AC上存在一点E,使ED与平面BCD成30°角.设
| CE |
| CA |
| m |
| m |
| DE |
|
| ||||
|
|
解答:解: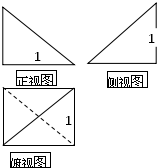 (1)在Rt△ABD中,AB=
(1)在Rt△ABD中,AB=
=
=
,
∵△ABC是正三角形,∴BC=AB=
.
∵BD=CD=1,∴BD2+CD2=BC2,
∴∠BDC=90°.
∴BD⊥CD.
如图所示,以BD,DC为邻边作正方形CDBP.
连接DP交AC于点O.连接AO.
则PD⊥CB,AO⊥CB.
又PD∩AO=O,∴CB⊥平面ADP.
∴平面APD⊥平面CDBP.
过点A作AF⊥OD,则AF⊥平面CDBP.
设AF=x,OF=y,
在Rt△AFD与Rt△AOF中,由勾股定理可得:
x2+y2=AO2=(
×
)2=
.x2+(y+
)2=(
)2.
解得y=
.
因此点F与点P重合.
据此可得:三棱锥A-BCD的三视图如右图所示:
(2)建立如图所示的空间直角坐标系.则P(0,0,0),A(0,0,1),B(-
,
,0),C(
,
,0),D(0,
,0).
∴
=(
,
,-1),
=(
,0,0),
=(0,
,-1).
设平面ABC的法向量为
=(x,y,z),
则
,取y=
,则x=0,z=1,∴
=(0,
,1).
同理,可求得平面ACD的一个法向量为
=(1,1,
).
∴cos<
,
>=
=
=
.
即二面角B-AC-D的余弦值为
.
(3)假设在线段AC上存在一点E,使ED与平面BCD成30°角.
设
=λ
,(0≤λ≤1),则
=(-
λ,-
λ,λ),∴E(
(1-λ),
(1-λ),λ),
∴
=(
(1-λ),-
(1+λ),λ).
取平面BCD的法向量为
=(0,0,1).
则sin30°=|cos<
,
>|=
=
=
,解得λ=
 (1)在Rt△ABD中,AB=
(1)在Rt△ABD中,AB=| AD2-BD2 |
(
|
| 2 |

∵△ABC是正三角形,∴BC=AB=
| 2 |
∵BD=CD=1,∴BD2+CD2=BC2,
∴∠BDC=90°.
∴BD⊥CD.
如图所示,以BD,DC为邻边作正方形CDBP.
连接DP交AC于点O.连接AO.
则PD⊥CB,AO⊥CB.
又PD∩AO=O,∴CB⊥平面ADP.
∴平面APD⊥平面CDBP.
过点A作AF⊥OD,则AF⊥平面CDBP.
设AF=x,OF=y,
在Rt△AFD与Rt△AOF中,由勾股定理可得:
x2+y2=AO2=(
| ||
| 2 |
| 2 |
| 3 |
| 2 |
| ||
| 2 |
| 3 |
解得y=
| ||
| 2 |
因此点F与点P重合.
据此可得:三棱锥A-BCD的三视图如右图所示:
(2)建立如图所示的空间直角坐标系.则P(0,0,0),A(0,0,1),B(-
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| 2 |
∴
| AC |
| ||
| 2 |
| ||
| 2 |
| BC |
| 2 |
| AD |
| 2 |
设平面ABC的法向量为
| n1 |
则
|
| 2 |
| n1 |
| 2 |
同理,可求得平面ACD的一个法向量为
| n2 |
| 2 |
∴cos<
| n1 |
| n2 |
| ||||
|
|
2
| ||
|
| ||
| 3 |
即二面角B-AC-D的余弦值为
| ||
| 3 |
(3)假设在线段AC上存在一点E,使ED与平面BCD成30°角.
设
| CE |
| CA |
| CE |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
∴
| DE |
| ||
| 2 |
| ||
| 2 |
取平面BCD的法向量为
| m |
则sin30°=|cos<
| m |
| DE |
|
| ||||
|
|
| λ | ||||||
|
| 1 |
| 2 |

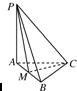 19、如图所示,在三棱锥P-ABC中,PA⊥平面ABC,AB=BC=CA=3,M为AB的中点,四点P、A、M、C都在球O的球面上.
19、如图所示,在三棱锥P-ABC中,PA⊥平面ABC,AB=BC=CA=3,M为AB的中点,四点P、A、M、C都在球O的球面上.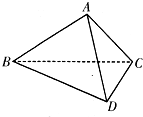 如图所示,在三棱锥A-BCD中,∠BDC为锐角,∠CBD=
如图所示,在三棱锥A-BCD中,∠BDC为锐角,∠CBD=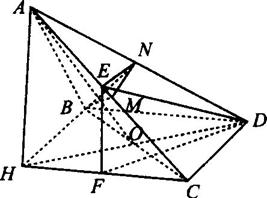
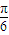 ,BC=
,BC=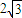 ,CD=AC=2,AB=AD=
,CD=AC=2,AB=AD=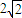 .
.