题目内容
 在三棱锥A-BCD中,AB=4,CD=2,且异面直线AB、CD所成的角为60°,若M、N分别是AD、BC的中点,则MN=
在三棱锥A-BCD中,AB=4,CD=2,且异面直线AB、CD所成的角为60°,若M、N分别是AD、BC的中点,则MN=| 3 |
| 7 |
| 3 |
| 7 |
分析:取AC的中点P,连接PM,PN,根据AB=4,CD=2,异面直线AB、CD所成的角为60°,利用三角形中位线定理求出PM,PN,进而利用余弦定理,可求出MN长.
解答:解:取AC的中点P连接PM,PN,
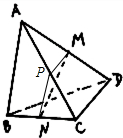
在△ABC中,PN∥AB且PN=
AB=2
在△ACD中,PM∥CD且PM=
CD=1
∵异面直线AB、CD所成的角为60°,
故∠NPM=60°或∠NPM=120°
当∠NPM=60°时,MN=
=
当∠NPM=120°时,MN=
=
故MN=
,或MN=
故答案为:
或

在△ABC中,PN∥AB且PN=
| 1 |
| 2 |
在△ACD中,PM∥CD且PM=
| 1 |
| 2 |
∵异面直线AB、CD所成的角为60°,
故∠NPM=60°或∠NPM=120°
当∠NPM=60°时,MN=
22+12-2•2•1•
|
| 3 |
当∠NPM=120°时,MN=
22+12+2•2•1•
|
| 7 |
故MN=
| 3 |
| 7 |
故答案为:
| 3 |
| 7 |
点评:本题主要考查了异面直线所成的角,空间中的线面关系,解三角形等基础知识,考查空间想象能力和思维能力.

练习册系列答案
相关题目
 如图,在三棱锥A-BCD中,DA,DB,DC两两垂直,且长度均为1,E为BC中点,则下列结论正确的是( )
如图,在三棱锥A-BCD中,DA,DB,DC两两垂直,且长度均为1,E为BC中点,则下列结论正确的是( ) (2011•渭南三模)在三棱锥A-BCD中,BD=BC=1,BD⊥BC,DE⊥AB,AD=2,AD⊥平面BCD.
(2011•渭南三模)在三棱锥A-BCD中,BD=BC=1,BD⊥BC,DE⊥AB,AD=2,AD⊥平面BCD. 如图所示,在三棱锥A-BCD中,侧面ABD、ACD是全等的直角三角形,AD是公共的斜
如图所示,在三棱锥A-BCD中,侧面ABD、ACD是全等的直角三角形,AD是公共的斜 如图,在三棱锥A-BCD中,平行于BC的平面MNPQ分别交AB、AC、CD、BD于M、N、P、Q四点,且MN=PQ.
如图,在三棱锥A-BCD中,平行于BC的平面MNPQ分别交AB、AC、CD、BD于M、N、P、Q四点,且MN=PQ.