题目内容
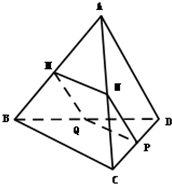 如图,在三棱锥A-BCD中,平行于BC的平面MNPQ分别交AB、AC、CD、BD于M、N、P、Q四点,且MN=PQ.
如图,在三棱锥A-BCD中,平行于BC的平面MNPQ分别交AB、AC、CD、BD于M、N、P、Q四点,且MN=PQ.(1)求证:四边形MNPQ为平行四边形;
(2)试在直线AC上找一点F,使得MF⊥AD.
分析:(1)由线面平行的性质得线线平行,进一步利用平行公理得线线平行,再由已知MN=PQ证得结论;
(2)先找一个过M且与AD垂直的面,面与AC的交点即为要找的F点.
(2)先找一个过M且与AD垂直的面,面与AC的交点即为要找的F点.
解答: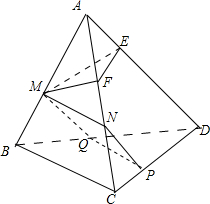 (1)证明:如图,
(1)证明:如图,
由已知BC∥平面MNPQ,BC?面ABC,面MNPQ∩面ABC=MN,
由线面平行的性质得,BC∥MN,
又BC∥平面MNPQ,BC?面BCD,面MNPQ∩面BCD=PQ,
由线面平行的性质得,BC∥PQ,
∴MN∥PQ,又由已知MN=PQ,∴四边形MNPQ为平行四边形;
(2)在面ABD中,过M作ME⊥AD,交AD于E,在面ACD中过E作EF⊥AD,交AC于F.
∵ME⊥AD,EF⊥AD,ME∩EF=E,
∴AD⊥面MEF,
∴MF⊥AD.
则AC上的点F为所求.
 (1)证明:如图,
(1)证明:如图,由已知BC∥平面MNPQ,BC?面ABC,面MNPQ∩面ABC=MN,
由线面平行的性质得,BC∥MN,
又BC∥平面MNPQ,BC?面BCD,面MNPQ∩面BCD=PQ,
由线面平行的性质得,BC∥PQ,
∴MN∥PQ,又由已知MN=PQ,∴四边形MNPQ为平行四边形;
(2)在面ABD中,过M作ME⊥AD,交AD于E,在面ACD中过E作EF⊥AD,交AC于F.
∵ME⊥AD,EF⊥AD,ME∩EF=E,
∴AD⊥面MEF,
∴MF⊥AD.
则AC上的点F为所求.
点评:本题考查了直线与平面垂直的性质,考查了空间直线与直线的位置关系,考查了学生的空间想象能力和思维能力,是中档题.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案
相关题目
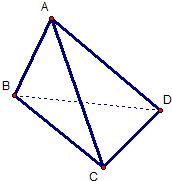 如图,在三棱锥A-BCD中,侧面ABD、ACD是全等的直角三角形,AD是公共的斜边,且AD=
如图,在三棱锥A-BCD中,侧面ABD、ACD是全等的直角三角形,AD是公共的斜边,且AD=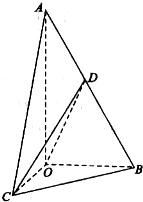 如图,在三棱锥A-BOC中,AO⊥底面BOC,∠OAB=∠OAC=30°,AB=AC=4,
如图,在三棱锥A-BOC中,AO⊥底面BOC,∠OAB=∠OAC=30°,AB=AC=4, 如图,在三棱锥A-BCD中,AD⊥平面ABC,∠BAC=120°,且AB=AC=AD=2,点E在BC上,且AE⊥AC.
如图,在三棱锥A-BCD中,AD⊥平面ABC,∠BAC=120°,且AB=AC=AD=2,点E在BC上,且AE⊥AC. 如图,在三棱锥A-BOC中,AO⊥面BOC,二面角B-AO-C是直二面角,OB=OC,
如图,在三棱锥A-BOC中,AO⊥面BOC,二面角B-AO-C是直二面角,OB=OC,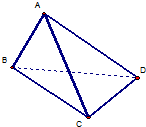 如图,在三棱锥A-BCD中,侧面ABD、ACD是全等的直角三角形,AD是公共的斜边,且AD=
如图,在三棱锥A-BCD中,侧面ABD、ACD是全等的直角三角形,AD是公共的斜边,且AD=