题目内容
 (2011•渭南三模)在三棱锥A-BCD中,BD=BC=1,BD⊥BC,DE⊥AB,AD=2,AD⊥平面BCD.
(2011•渭南三模)在三棱锥A-BCD中,BD=BC=1,BD⊥BC,DE⊥AB,AD=2,AD⊥平面BCD.(Ⅰ)求证:DE⊥平面ABC;
(Ⅱ)求平面BAC与平面DAC夹角的余弦值.
分析:(Ⅰ)证明DE⊥平面ABC,由于DE⊥AB,只需证明DE⊥BC,利用AD⊥平面BCD,BD⊥BC,可以证明BC⊥平面ABD,从而问题得证;
(Ⅱ)过点D作DF⊥AC,连接EF,根据DE⊥平面ABC,可知∠DFE为平面BAC与平面DAC夹角,分别计算出EF,DF的长,再利用余弦函数即可求得.
(Ⅱ)过点D作DF⊥AC,连接EF,根据DE⊥平面ABC,可知∠DFE为平面BAC与平面DAC夹角,分别计算出EF,DF的长,再利用余弦函数即可求得.
解答:(Ⅰ)证明:∵AD⊥平面BCD,BC?平面BCD
∴AD⊥BC
∵BD⊥BC,BD∩AD=D
∴BC⊥平面ABD
∵DE?平面ABD
∴DE⊥BC
∵DE⊥AB,AB∩BC=B
∴DE⊥平面ABC;
(Ⅱ)过点D作DF⊥AC,连接EF,则
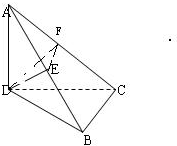
∵DE⊥平面ABC,
∴EF⊥AC
∴∠DFE为平面BAC与平面DAC夹角
在直角△ADC中,AD=2,DC=
,∴AC=
,∵AD×DC=AC×DF,∴DF=
在直角△ADC中,AD=2,BD=1,∴AB=
,∵AD×DB=AB×DE,∴DE=
∴EF=
∴cos∠DFE=
=
∴AD⊥BC
∵BD⊥BC,BD∩AD=D
∴BC⊥平面ABD
∵DE?平面ABD
∴DE⊥BC
∵DE⊥AB,AB∩BC=B
∴DE⊥平面ABC;
(Ⅱ)过点D作DF⊥AC,连接EF,则

∵DE⊥平面ABC,
∴EF⊥AC
∴∠DFE为平面BAC与平面DAC夹角
在直角△ADC中,AD=2,DC=
| 2 |
| 6 |
2
| ||
| 3 |
在直角△ADC中,AD=2,BD=1,∴AB=
| 5 |
2
| ||
| 5 |
∴EF=
|
∴cos∠DFE=
| EF |
| DF |
| ||
| 5 |
点评:本题以三棱锥为载体,考查线面垂直,解题的关键是正确理解与运用线面垂直的判定与性质,求面面角的关键是正确作出面面角

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
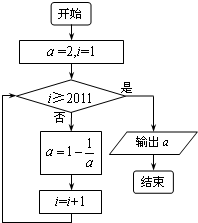 (2011•渭南三模)已知某程序框图如图所示,则执行该程序后输出的结果是( )
(2011•渭南三模)已知某程序框图如图所示,则执行该程序后输出的结果是( ) (2011•渭南三模)已知正三棱柱的侧面积为36,其三视图如图所示,则它的左视图的面积为( )
(2011•渭南三模)已知正三棱柱的侧面积为36,其三视图如图所示,则它的左视图的面积为( )