题目内容

如图，在三棱锥A-BCD中，DA，DB，DC两两垂直，且长度均为1，E为BC中点，则下列结论正确的是（　　）
分析：依据已知条件，结合立体几何中相关的定理及结论对四个选项逐一验证，即可得到正确结论．
解答：解：由于DA，DB，DC两两垂直，且长度均为1，则△ABC为边长是
2
的等边三角形．
又由E为BC中点，则AE=
AB2-BE2
=
(
2
)2-(
2
2
)2
=
3
2
≠
3
2
，故A错；
由于DE与平面ABD不垂直，故∠EAD不是AE与平面ABD所成的角，故B错；
若DE为点D到平面ABC的距离，则DE⊥平面ABC，故∠AED为直角，而在三角形ADE中，∠ADE为直角，矛盾，故C错；
由于E为BC中点，则AE⊥BC，DE⊥BC，故∠AED为二面角A-BC-D的平面角，故D正确
故答案为 D
点评：本题给出三棱锥有三条棱两两垂直，着重考查了线面垂直，线面角，面面角等知识点，属于基础题．
练习册系列答案
相关题目
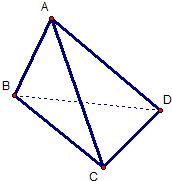精英家教网如图，在三棱锥A-BCD中，侧面ABD、ACD是全等的直角三角形，AD是公共的斜边，且AD=
3
，BD=CD=1，另一个侧面是正三角形．
（1）求证：AD⊥BC．
（2）求二面角B-AC-D的大小．
（3）在直线AC上是否存在一点E，使ED与面BCD成30°角？若存在，确定E的位置；若不存在，说明理由．
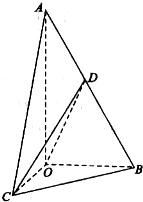精英家教网如图，在三棱锥A-BOC中，AO⊥底面BOC，∠OAB=∠OAC=30°，AB=AC=4，BC=2
2
，动点D在线段AB上．
（Ⅰ）求证：平面COD⊥平面AOB；
（Ⅱ）当点D运动到线段AB的中点时，求二面角D-CO-B的大小；
（Ⅲ）当CD与平面AOB所成角最大时，求三棱锥C-OBD的体积．
如图，在三棱锥A-BCD中，AD⊥平面ABC，∠BAC=120°，且AB=AC=AD=2，点E在BC上，且AE⊥AC．
（Ⅰ）求证：AC⊥DE；
（Ⅱ）求点B到平面ACD的距离．
如图，在三棱锥A-BOC中，AO⊥面BOC，二面角B-AO-C是直二面角，OB=OC，∠OAB=
π6
，斜边AB=4，动点D在斜边AB上．
（1）求证：平面COD⊥平面AOB；
（2）当D为AB的中点时，求：异面直线AO与CD所成角大小．
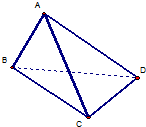如图，在三棱锥A-BCD中，侧面ABD、ACD是全等的直角三角形，AD是公共的斜边，且AD=
3
，BD=CD=1，另一个侧面是正三角形
（1）求证：AD⊥BC
（2）求二面角B-AC-D的大小．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网