题目内容
已知a为常数,求函数f(x)=x(3a-x2),x∈[0,1]的最大值.
考点:函数的最值及其几何意义
专题:导数的概念及应用
分析:求函数f(x)=x(3a-x2)=-x3+3ax的导数,对方程f'(x)=-3(x2-a)=0有无实根,和有根,根是否在区间[0,1]内进行讨论,求得函数的极值,再与f(0)、f(1)比较大小,确定函数的最大值.
解答:
解:f'(x)=-3x2+3a=-3(x2-a)
若a≤0,则f'(x)=-3(x2-a)≤0,此时函数f(x)单调递减,
所以当x=0时,f(x)取得最大值,f(x)max=f(0)=0
若a>0,令f'(x)=-3(x2-a)=0,解得x=±
,
∵x∈[0,1],则只考虑x=
的情况,
①当0<a<1时,根据函数的增减性得,
当x=
时,f(x)有最大值,f(x)max=f(
)=2a
;
②当
≥1,即a≥1时,根据函数的增减性得
当x=1时,f(x)有最大值.f(x)max=f(1)=3a-1.
综合以上可知:
当a≤0时,x=0,f(x)有最大值0;
当0<a<1时,x=
,f(x)有最大值2a
;
当a≥1时,x=1,f(x)有最大值3a-1.
若a≤0,则f'(x)=-3(x2-a)≤0,此时函数f(x)单调递减,
所以当x=0时,f(x)取得最大值,f(x)max=f(0)=0
若a>0,令f'(x)=-3(x2-a)=0,解得x=±
| a |
∵x∈[0,1],则只考虑x=
| a |
①当0<a<1时,根据函数的增减性得,
当x=
| a |
| a |
| a |
②当
| a |
当x=1时,f(x)有最大值.f(x)max=f(1)=3a-1.
综合以上可知:
当a≤0时,x=0,f(x)有最大值0;
当0<a<1时,x=
| a |
| a |
当a≥1时,x=1,f(x)有最大值3a-1.
点评:考查利用导数研究函数在闭区间上的最值问题,对方程f'(x)=0有无实根,和有根,根是否在区间[0,1]内进行讨论,体现了分类讨论的思想方法,增加了题目的难度,属中档题.

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
若tanx=2则cos2x=( )
A、-
| ||
B、
| ||
C、
| ||
D、-
|
已知a=log
3,b=log
2,c=20.3,则a,b,c三者的大小关系是( )
| 1 |
| 2 |
| 1 |
| 2 |
| A、c>b>a |
| B、a>c>b |
| C、b>a>c |
| D、c>a>b |
设a、b∈R,已知命题p:a2+b2≤2ab,命题q:(
)2≤
,p是q成立的( )
| a+b |
| 2 |
| a2+b2 |
| 2 |
| A、必要不充分条件 |
| B、充分不必要条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
下列结论正确的是( )
| A、在同一直角坐标系中,函数y=sinx的图象和函数y=x的图象有三个公共点 | ||||||||||||
B、已知向量
| ||||||||||||
| C、在△ABC中,A>B的充要条件是sinA>sinB | ||||||||||||
D、从总体中随机抽出一个容量为20的样本,其数据的分组及各组的频数如下表,则估计总体的中位数为18
|
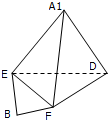 如图,边长为2的正方形ABCD中,E是AB边上的点,F是边BC上的点,且BE=BF,若将△AED、△DCF分别沿DE、DF折起,使A、C两点重合于点A1.
如图,边长为2的正方形ABCD中,E是AB边上的点,F是边BC上的点,且BE=BF,若将△AED、△DCF分别沿DE、DF折起,使A、C两点重合于点A1.