题目内容
求下列函数的定义域:
(1)y=21-x;
(2)y=
;
(3)y=
.
(1)y=21-x;
(2)y=
| 1 |
| 9-3x |
(3)y=
| 1-2x |
考点:函数的定义域及其求法
专题:函数的性质及应用
分析:(1)由函数y=2x的定义域为R可得所求函数的定义域;
(2)分母不为0即可解出;
(3)根据被开方数≥0可得原函数的定义域.
(2)分母不为0即可解出;
(3)根据被开方数≥0可得原函数的定义域.
解答:
解:(1)∵根据指数函数的定义域为R,即可得函数y=21-x的定义域也为R;
(2)要使函数有意义,x需满足:9-3x≠0,解得x≠2,
∴函数y=
的定义域为(-∞,2)∪(2,+∞)
(3))要使函数有意义,x需满足:1-2x≥0,解得x≤0,
∴函数y=
的定义域为(-∞,0]
(2)要使函数有意义,x需满足:9-3x≠0,解得x≠2,
∴函数y=
| 1 |
| 9-3x |
(3))要使函数有意义,x需满足:1-2x≥0,解得x≤0,
∴函数y=
| 1-2x |
点评:本题主要考查函数定义域的求解,根据指数函数的性质及分母不为0、偶次方根的被开方数大于等于0是解决本题的关键.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
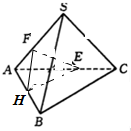 如图,一个四面体S-ABC的六条棱长都为4,E为SA的中点,过点E作平面EFH∥平面SBC.且平面EFH∩平面ABC=FH,则△HFE面积为
如图,一个四面体S-ABC的六条棱长都为4,E为SA的中点,过点E作平面EFH∥平面SBC.且平面EFH∩平面ABC=FH,则△HFE面积为