题目内容
【题目】圆![]() 的方程为:
的方程为:![]() ,
,![]() 为圆上任意一点,过
为圆上任意一点,过![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,点
,点![]() 在
在![]() 上,且
上,且![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过点![]() 的直线与曲线
的直线与曲线![]() 交于
交于![]() 、
、![]() 两点,点
两点,点![]() 的坐标为
的坐标为![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() 的最大值,及直线
的最大值,及直线![]() 的方程.
的方程.
【答案】(1)![]() (2)
(2)![]() ,直线
,直线![]() 的方程为
的方程为![]() 或
或![]() .
.
【解析】
(1)设点![]() 的坐标
的坐标![]() ,求出
,求出![]() 的坐标,设
的坐标,设![]() ,通过
,通过![]() ,可以得到
,可以得到
![]() 与
与![]() 的关系,
的关系,![]() 与
与![]() 的关系,把
的关系,把![]() 代入圆的方程中,最后得到点
代入圆的方程中,最后得到点![]() 的轨迹
的轨迹![]() 的方程。
的方程。
(2)由题意易知直线的斜率不为0,设直线![]() 的方程为
的方程为![]() ,直线方程与点
,直线方程与点![]() 的轨迹
的轨迹![]() 的方程联立,根据一元二次方程根与系数关系,可以得出
的方程联立,根据一元二次方程根与系数关系,可以得出![]() 的面积
的面积![]() 的表达式,最后利用基本不等式可以求出
的表达式,最后利用基本不等式可以求出![]() 的最大值,直线
的最大值,直线![]() 的方程.
的方程.
(1)设![]() ,则
,则![]() ,设
,设![]() ,
,![]() ,
,![]() ,因为
,因为![]() ,所以
,所以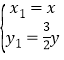 ,把
,把![]() 代入圆的方程得
代入圆的方程得![]() ,所以
,所以![]() 的轨迹
的轨迹![]() 的方程为
的方程为![]() .
.
(2)由题意易知直线的斜率不为0,设直线![]() 的方程为
的方程为![]() ,设
,设![]() ,
,![]() ,
,
联立![]() ,
,![]() ,
,![]() ,
,
![]()
![]()
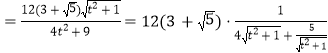
![]() .
.
当且仅当![]() 时取等号,
时取等号,
所以![]() 面积有最大值为
面积有最大值为![]() .
.
所以![]() 的面积为最大时,直线
的面积为最大时,直线![]() 的方程为
的方程为![]() 或
或![]() .
.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目