题目内容
已知在四棱锥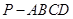 中,底面
中,底面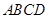 是矩形,且
是矩形,且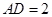 ,
,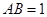 ,
,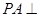 平面
平面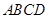 ,
,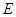 、
、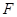 分别是线段
分别是线段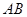 、
、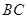 的中点.
的中点.
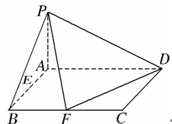
(1)证明: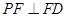 ;
;
(2)判断并说明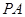 上是否存在点
上是否存在点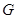 ,使得
,使得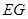 ∥平面
∥平面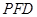 ;
;
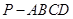 中,底面
中,底面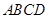 是矩形,且
是矩形,且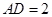 ,
,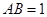 ,
,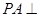 平面
平面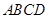 ,
,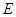 、
、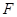 分别是线段
分别是线段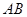 、
、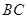 的中点.
的中点.
(1)证明:
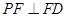 ;
;(2)判断并说明
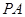 上是否存在点
上是否存在点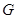 ,使得
,使得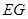 ∥平面
∥平面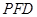 ;
;(1)证明:见解析;(2)满足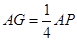 的点
的点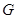 即为所求.
即为所求.
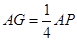 的点
的点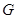 即为所求.
即为所求.试题分析:(1)通过
 ,证明得到
,证明得到 再利用
再利用 ,∴
,∴ ,推出“线线垂直”.
,推出“线线垂直”.(2)注意运用已有的“平行关系”:过点
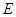 作
作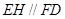 交
交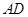 于点
于点 ,则
,则 ∥平面
∥平面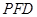 ,
,且有
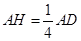 ,再过点
,再过点 作
作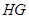 ∥
∥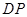 交
交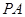 于点
于点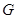 ,得到
,得到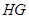 ∥平面
∥平面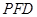 且
且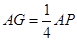 ,
,根据平面
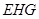 ∥平面推出
∥平面推出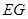 ∥平面
∥平面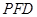 .
.从而作出结论:满足
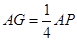 的点
的点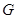 即为所求.
即为所求.试题解析:证明:连接
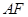 ,则
,则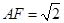 ,
, ,
,又
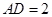 ,
,∴
 ,∴
,∴ 3分
3分又
 ,∴
,∴ ,又
,又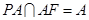 ,
,∴
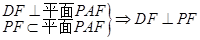 6分
6分(2)过点
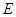 作
作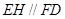 交
交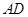 于点
于点 ,则
,则 ∥平面
∥平面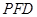 ,
,且有
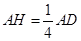 8分
8分再过点
 作
作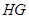 ∥
∥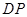 交
交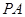 于点
于点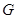 ,则
,则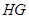 ∥平面
∥平面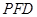 且
且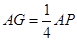 ,
,∴ 平面
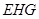 ∥平面
∥平面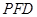 10分
10分∴
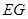 ∥平面
∥平面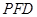 .
.从而满足
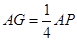 的点
的点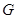 即为所求. 12分
即为所求. 12分
练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
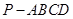 的底面是边长为1的正方形,
的底面是边长为1的正方形, ,点E在棱PB上.
,点E在棱PB上.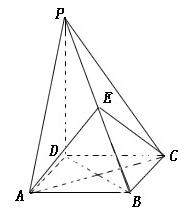
 ;
;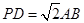 且E为PB的中点时,求AE与平面PDB
且E为PB的中点时,求AE与平面PDB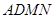 都为正方形,
都为正方形,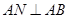 ,F
,F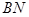 的中点,E为线段BC上的动点.
的中点,E为线段BC上的动点.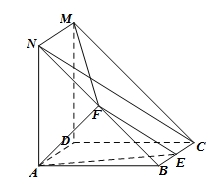
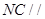 平面AEF;
平面AEF;
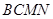 平面;
平面;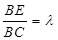 ,写出
,写出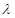 为何值时MF⊥平面AEF(结论不要求证明).
为何值时MF⊥平面AEF(结论不要求证明).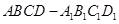 中,
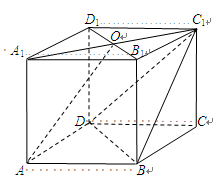
中,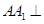 底面
底面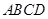 ,底面
,底面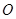 为
为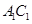 与
与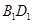 交点,已知
交点,已知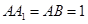 ,
,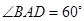 .
.
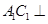 平面
平面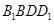 ;
;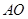 ∥平面
∥平面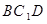 ;
;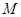 在
在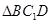 内(含边界),且
内(含边界),且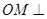
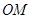 的最小值.
的最小值.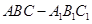 中,
中,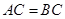 ,
,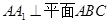 ,点
,点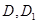 分别是
分别是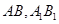 的中点.
的中点.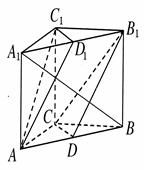
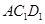 ∥平面
∥平面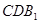 ;
;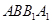 ;
;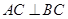 ,
,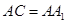 ,求异面直线
,求异面直线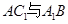 所成的角。
所成的角。 A1B1C1,
A1B1C1,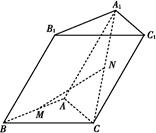


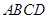 沿对角线
沿对角线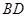 折成直二面角
折成直二面角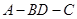 ,有如下四个结论:
,有如下四个结论: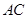 ⊥
⊥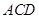 是等边三角形;③
是等边三角形;③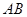 与平面
与平面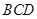 所成的角为60°;
所成的角为60°;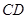 所成的角为60°.其中错误的结论是
所成的角为60°.其中错误的结论是