题目内容
已知如图①所示,矩形纸片AA′A1′A1,点B、C、B1、C1分别为AA′、A1A1′的三等分点,将矩形纸片沿BB1、CC1折成如图②形状(正三棱柱),若面对角线AB1⊥BC1,求证:A1C⊥AB1.

(图①)

(图②)

(图①)

(图②)
见解析
作AD∥BC,BD∥AC交于D,作A1D1∥B1C1,B1D1∥A1C1交于D1.
连结BD1、DD1
∵A1C1B1D1为菱形,∴A1B1⊥D1C1.
又AA1⊥平面A1D1B1C1,∴AA1⊥D1C1.
又D1C1⊥平面ABB1A1,∴D1C1⊥AB1.
又AB1⊥BC1,∴AB1⊥平面BC1D1,∴AB1⊥BD1.
又BD1∥CA1,∴AB1⊥A1C.
连结BD1、DD1
∵A1C1B1D1为菱形,∴A1B1⊥D1C1.
又AA1⊥平面A1D1B1C1,∴AA1⊥D1C1.
又D1C1⊥平面ABB1A1,∴D1C1⊥AB1.
又AB1⊥BC1,∴AB1⊥平面BC1D1,∴AB1⊥BD1.
又BD1∥CA1,∴AB1⊥A1C.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
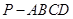 中,底面
中,底面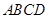 是矩形,且
是矩形,且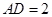 ,
,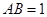 ,
,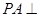 平面
平面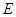 、
、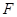 分别是线段
分别是线段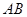 、
、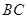 的中点.
的中点.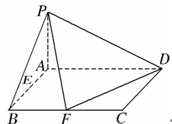
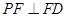 ;
;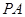 上是否存在点
上是否存在点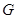 ,使得
,使得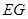 ∥平面
∥平面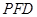 ;
;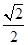 AD.若E、F分别为PC、BD的中点,求证:
AD.若E、F分别为PC、BD的中点,求证: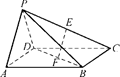
 ,
, ,
, ,则两直线PC与AB所成角的大小是______.
,则两直线PC与AB所成角的大小是______.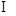 β,且α⊥β,则l⊥α;
β,且α⊥β,则l⊥α;