题目内容
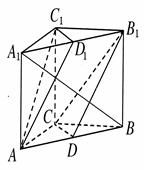
如图所示,在三棱柱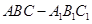 中,
中,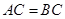 ,
,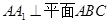 ,点
,点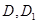 分别是
分别是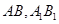 的中点.
的中点.
(1)求证:平面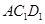 ∥平面
∥平面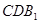 ;
;
(2)求证:平面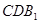 ⊥平面
⊥平面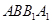 ;
;
(3)若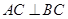 ,
,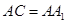 ,求异面直线
,求异面直线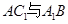 所成的角。
所成的角。
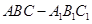 中,
中,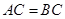 ,
,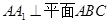 ,点
,点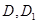 分别是
分别是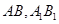 的中点.
的中点.
(1)求证:平面
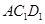 ∥平面
∥平面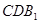 ;
;(2)求证:平面
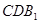 ⊥平面
⊥平面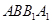 ;
;(3)若
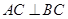 ,
,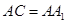 ,求异面直线
,求异面直线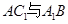 所成的角。
所成的角。(1) 详见解析(2) 详见解析(3)详见解析
试题分析:(1)根据平面几何可证
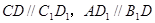 ,可证得面面垂直;(2)根据D是AB的中点,可证
,可证得面面垂直;(2)根据D是AB的中点,可证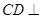 面
面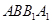 ,证得面面垂直;(3)异面直线所成的角,转化成相交直线所成的角,然后在所在三角形内解决角的问题.
,证得面面垂直;(3)异面直线所成的角,转化成相交直线所成的角,然后在所在三角形内解决角的问题.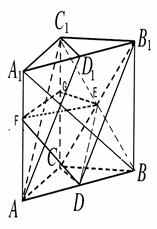
试题解析:解:(1)证明:在直三棱柱ABC-A1B1C1中,∵点D,D1分别是AB,A1B1的中点,D1B1
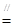 AD∴四边形ADB1D1为平行四边形∴AD1∥DB1∵AD1
AD∴四边形ADB1D1为平行四边形∴AD1∥DB1∵AD1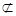 平面CDB1∴AD1//平面CDB1,同理可证C1D1∥平面CDB1∵AD1
平面CDB1∴AD1//平面CDB1,同理可证C1D1∥平面CDB1∵AD1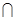 D1C1=D1∴平面AC1D1∥平面CDB 4分
D1C1=D1∴平面AC1D1∥平面CDB 4分(2)证明:∵AA1⊥平面ABC,CD
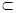 平面ABC∴AA1⊥CD。∵AC=BC
平面ABC∴AA1⊥CD。∵AC=BCD是AB的中点∴CD⊥AB∵AA1
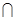 AB=A∴CD⊥平面ABB1A1
AB=A∴CD⊥平面ABB1A1∵CD
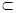 平面ABC∴平面CDB1⊥平面ABB1A1 9分
平面ABC∴平面CDB1⊥平面ABB1A1 9分(3)连接BC1交B1C于E,连接DE,取AA1中点F,连接EF,又∵D是AB中点,∴AC1 ∥DE,DF∥A1B ∴ ∠EDF是异面直线
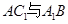 所成的角。设AC=1DE=
所成的角。设AC=1DE=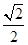 ,DF=
,DF=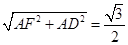 ,EF
,EF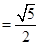 ∴DE2+ DF2= EF2∴∠EDF=90O∴异面直线
∴DE2+ DF2= EF2∴∠EDF=90O∴异面直线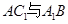 所成的角为90O。13分
所成的角为90O。13分也可能证明
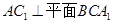 也可得异面直线
也可得异面直线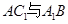 所成的角为90O 13分
所成的角为90O 13分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
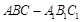 中,侧面
中,侧面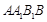 为菱形,且
为菱形,且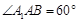 ,
,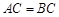 ,
,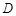 是
是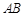 的中点.
的中点.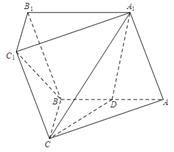
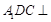 平面
平面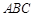 ;
;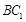 ∥平面
∥平面 .
.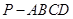 中,底面
中,底面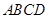 是矩形,且
是矩形,且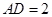 ,
,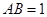 ,
,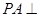 平面
平面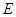 、
、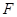 分别是线段
分别是线段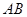 、
、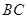 的中点.
的中点.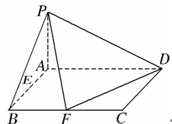
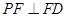 ;
;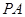 上是否存在点
上是否存在点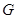 ,使得
,使得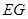 ∥平面
∥平面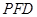 ;
; 中,底面
中,底面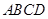 是矩形,
是矩形, 平面
平面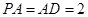 ,
, ,
,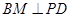 于点
于点 .
.

 ;
; 与平面
与平面 所成的角的余弦值.
所成的角的余弦值.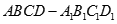 中,下列几种说法错误的是
中,下列几种说法错误的是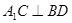
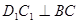
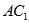 与
与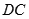 成
成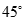 角
角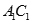 与
与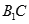 成
成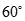 角
角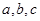 表示不同直线,M表示平面,给出四个命题:①若
表示不同直线,M表示平面,给出四个命题:①若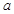 ∥M,
∥M,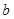 ∥M,则
∥M,则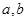 相交或
相交或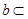 M,
M,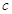 ,
, ,
, ,
, ,则两直线PC与AB所成角的大小是______.
,则两直线PC与AB所成角的大小是______.