题目内容
【题目】极坐标系中椭圆C的方程为![]() ,以极点为原点,极轴为
,以极点为原点,极轴为![]() 轴非负半轴,建立平面直角坐标系,且两坐标系取相同的单位长度.
轴非负半轴,建立平面直角坐标系,且两坐标系取相同的单位长度.
(Ⅰ)求该椭圆的直角标方程,若椭圆上任一点坐标为![]() ,求
,求![]() 的取值范围;
的取值范围;
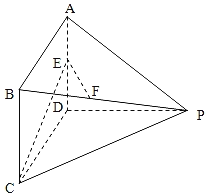
(Ⅱ)若椭圆的两条弦![]() ,
,![]() 交于点
交于点![]() ,且直线
,且直线![]() 与
与![]() 的倾斜角互补,求证:
的倾斜角互补,求证:![]() .
.
【答案】(Ⅰ)![]() ;(Ⅱ)证明见解析
;(Ⅱ)证明见解析
【解析】
(Ⅰ)将椭圆的极坐标方程化为直角坐标方程,即可设![]() ,
,![]() ,则
,则![]() ,进而求解;
,进而求解;
(Ⅱ)设直线![]() 的倾斜角为
的倾斜角为![]() ,直线
,直线![]() 的倾斜角为
的倾斜角为![]() ,
,![]() ,将直线
,将直线![]() 的参数方程代入椭圆的直角坐标方程中,由韦达定理可得
的参数方程代入椭圆的直角坐标方程中,由韦达定理可得![]() ,设
,设![]() 、
、![]() 对应参数分别为
对应参数分别为![]() 、
、![]() ,则
,则![]() ,同理可求得
,同理可求得![]() ,即可得证.
,即可得证.
(Ⅰ)由已知,![]() ,即
,即![]() ,
,
所以该椭圆的直角坐标方程为![]() ,
,
设![]() ,
,![]() ,
,
所以![]() ,
,
所以![]() 的取值范围是
的取值范围是![]()
(Ⅱ)证明:设直线![]() 的倾斜角为
的倾斜角为![]() ,直线
,直线![]() 的倾斜角为
的倾斜角为![]() ,
,![]()
则直线![]() 的参数方程为
的参数方程为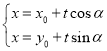 (
(![]() 为参数),
为参数),
代入![]() 得
得![]() ,
,
即![]() ,
,
设![]() 、
、![]() 对应参数分别为
对应参数分别为![]() 、
、![]() ,则
,则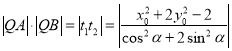 ,
,
同理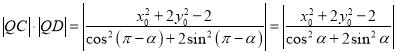 ,
,
所以![]()

练习册系列答案
 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目