题目内容
8.等差数列{an}中,a1>0,公差d<0,Sn为其前n项和,对任意自然数n,若点(n,Sn)在以下4条曲线中的某一条上,则这条曲线应是( )| A. | 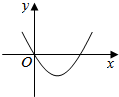 | B. |  | C. | 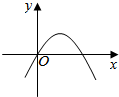 | D. | 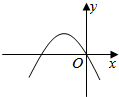 |
分析 等差数列的前n项和,等价于二次函数,根据二次函数的图象和性质即可到答案.
解答 解:∵等差数列{an}中,a1>0,公差d<0,Sn为其前n项和,
∴Sn=na1+$\frac{n(n-1)}{2}$×d=$\frac{d}{2}$n2+(a1-$\frac{d}{2}$)n,
∴点(n,Sn)在曲线y=$\frac{d}{2}$x2+(a1-$\frac{d}{2}$)x,
∵d<0,
∴二次函数开口向下,
∵对称轴x=-$\frac{{a}_{1}-\frac{d}{2}}{d}$>0,
∴对称轴在y轴的右侧,
故选:C.
点评 本题考查了等差数列的求和公式以及二次函数的性质,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.如果点M(sinθ,cosθ)位于第二象限,那么角θ所在的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
16.2014年国家加大对科技创新行业的支持力度,某研究机构对一新型行业的企业年投入x(单位:万元)与年盈利y(单位:万元)情况进行了统计分析,得下表数据:
根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程$\widehat{y}$=bx+a中的b的值为0.7,若某企业计划年投资14万元,则该企业的年盈利约为( )
| x | 6 | 8 | 10 | 12 |
| y | 2 | 3 | 5 | 6 |
| A. | 6.5 | B. | 7 | C. | 7.5 | D. | 8 |
13.在等比数列{an}中,a3=7,前3项之和S3=21,则公比q的值等于( )
| A. | 1 | B. | -$\frac{1}{2}$ | C. | 1或$-\frac{1}{2}$ | D. | -1或$\frac{1}{2}$ |
20.已知f(x)=log2(x2-ax+3a)在[2,+∞)上是增函数,则实数a的取值范围是( )
| A. | (-∞,4) | B. | (-4,4] | C. | (-∞,-4)∪[2,+∞) | D. | [-4,4) |
17.复数$z=3i+\frac{2}{1+i}$(i是虚数单位)在复平面内对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
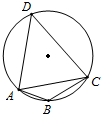 在半径为R的圆的内接四边形ABCD中,AB=2,BC=4,∠ABC=120°,AD+CD=10.求:
在半径为R的圆的内接四边形ABCD中,AB=2,BC=4,∠ABC=120°,AD+CD=10.求: