题目内容
13.在等比数列{an}中,a3=7,前3项之和S3=21,则公比q的值等于( )| A. | 1 | B. | -$\frac{1}{2}$ | C. | 1或$-\frac{1}{2}$ | D. | -1或$\frac{1}{2}$ |
分析 根据题意和等比数列的通项公式列出方程组,求出公比q的值.
解答 解:∵在等比数列{an}中,a3=7,S3=21,
∴$\left\{\begin{array}{l}{{a}_{1}{q}^{2}=7}\\{{a}_{1}+{a}_{1}q+{a}_{1}{q}^{2}=21}\end{array}\right.$,化简得2q2-q-1=0,
解得q=1或$-\frac{1}{2}$,
故选:C.
点评 本题考查等比数列的通项公式,以及方程思想,若利用等比数列的前n项和公式遗忘q=1的情况,属于基础题.

练习册系列答案
相关题目
1.刘徽在他的《九章算术注》中提出一个独特的方法来计算球体的体积:他不直接给出球体的体积,而是先计算另一个叫“牟合方盖”的立体的体积.刘徽通过计算,“牟合方盖”的体积与球的体积之比应为4:π,即V牟:V球=4:π.也导出了“牟合方盖”的$\frac{1}{8}$体积计算公式,即$\frac{1}{8}$V牟=r3-V方盖差,从而计算出V球=$\frac{4}{3}π{r^3}$.记所有棱长都为r的正四棱锥的体积为V正,则( )
| A. | V方盖差>V正 | B. | V方盖差=V正 | ||
| C. | V方盖差<V正 | D. | 以上三种情况都有可能 |
18.已知三棱锥S-ABC的所有顶点都在球O的球面上,SA⊥平面ABC,SA=2$\sqrt{3}$,AB=1,AC=2,$∠BAC=\frac{π}{3}$,则球O的表面积为( )
| A. | 16π | B. | 12π | C. | 8π | D. | 4π |
5.一个物体的运动方程为s(t)=sint,则它在$t=\frac{π}{3}$时的速度为( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{π}{3}$ |
2.已知直线l与椭圆$\frac{x^2}{4}+\frac{y^2}{2}=1$交于A、B两点,弦AB的中点为P(1,1),则直线l的方程是( )
| A. | x+2y-3=0 | B. | 2x+y-3=0 | C. | 2x-y-1=0 | D. | x-2y+1=0 |
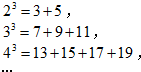 已知大于1的任意一个自然数的三次幂都可写成连续奇数的和.如:
已知大于1的任意一个自然数的三次幂都可写成连续奇数的和.如: