题目内容
【题目】在五边形AEBCD中,![]() ,C
,C![]() ,
,![]() ,
,![]() ,
,![]() (如图).将△ABE沿AB折起,使平面ABE⊥平面ABCD,线段AB的中点为O(如图).
(如图).将△ABE沿AB折起,使平面ABE⊥平面ABCD,线段AB的中点为O(如图).
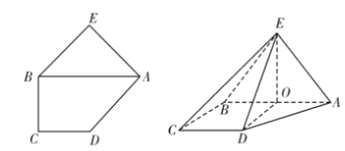
(1)求证:平面ABE⊥平面DOE;
(2)求平面EAB与平面ECD所成的锐二面角的大小.
【答案】(1)见解析(2)45°
【解析】
(1)根据矩形的性质,求得![]() ,再由等腰三角形的性质,证得
,再由等腰三角形的性质,证得![]() ,由线面垂直的判定,可得AB⊥平面EOD,再由面面垂直的判定定理,即可证得平面ABE⊥平面EOD;
,由线面垂直的判定,可得AB⊥平面EOD,再由面面垂直的判定定理,即可证得平面ABE⊥平面EOD;
(2)由(1)以O为坐标原点,以OB,OD,OE所在直线分别为![]() 轴建立如图所示的空间直角坐标系
轴建立如图所示的空间直角坐标系![]() ,求得平面ECD和平面ABE的法向量,利用向量的夹角公式,即可求解.
,求得平面ECD和平面ABE的法向量,利用向量的夹角公式,即可求解.
(1)由题意![]() ,O是线段AB的中点,则
,O是线段AB的中点,则![]() .
.
又![]() ,则四边形OBCD为平行四边形,又
,则四边形OBCD为平行四边形,又![]() ,则
,则![]() ,
,
因![]() ,
,![]() ,则
,则![]() .
.
![]() ,则AB⊥平面EOD.
,则AB⊥平面EOD.
又![]() 平面ABE,故平面ABE⊥平面EOD.
平面ABE,故平面ABE⊥平面EOD.
(2)由(1)易知OB,OD,OE两两垂直,以O为坐标原点,以OB,OD,OE所在直线分别为![]() 轴建立如图所示的空间直角坐标系
轴建立如图所示的空间直角坐标系![]() ,
,
△EAB为等腰直角三角形,且AB=2CD=2BC,
则![]() ,取
,取![]() ,
,
则O(0,0,0),A(-1,0,0),B(1,0,0),C(1,1,0),D(0,1,0),
E(0,0,1),则![]() ,
,![]() ,
,
设平面ECD的法向量为![]() ,
,
则有取
![]()
![]() ,得平面ECD的一个法向量
,得平面ECD的一个法向量![]() ,
,
因OD⊥平面ABE.则平面ABE的一个法向量为![]() ,
,
设平面ECD与平面ABE所成的锐二面角为θ,则
![]() ,
,
因为![]() ,所以
,所以![]() ,
,
故平面ECD与平面ABE所成的镜二面角为45°.


练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目