题目内容
在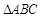 中,已知
中,已知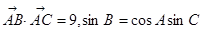 ,又
,又 的面积等于6.
的面积等于6.
(Ⅰ)求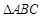 的三边之长;
的三边之长;
(Ⅱ)设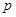 是
是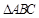 (含边界)内一点,
(含边界)内一点,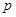 到三边
到三边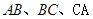 的距离分别为
的距离分别为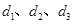 ,求
,求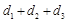 的取值范围.
的取值范围.
(Ⅰ)三边长分别为3,4,5.(Ⅱ)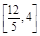 .
.
解析试题分析:(Ⅰ)对条件 ,由正弦定理和余弦定理可以转化为只含边的等式,这个等式
,由正弦定理和余弦定理可以转化为只含边的等式,这个等式
化简后为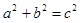 ,由此得
,由此得 ,所以
,所以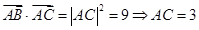 .再根据三角形的面积等于6可得BC=4,由勾股定理可得AB=5.
.再根据三角形的面积等于6可得BC=4,由勾股定理可得AB=5.
(Ⅱ)以C为坐标原点,射线CA为x轴正半轴建立直角坐标系,设P点坐标为(x, y),则由点到直线的距离公式可将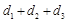 用点P的坐标表示出来,然后用线性规划可求出其取值范围.
用点P的坐标表示出来,然后用线性规划可求出其取值范围.
试题解析:(Ⅰ)法一、设三角形三内角A、B、C对应的三边分别为a, b, c,
∵ ,∴
,∴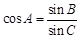 ,由正弦定理有
,由正弦定理有 ,
,
又由余弦定理有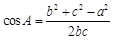 ,∴
,∴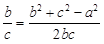 ,即
,即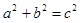 ,
,
所以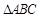 为Rt
为Rt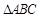 ,且
,且 3分
3分
所以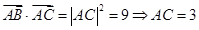
又 ,由勾股定理可得AB=5 6分
,由勾股定理可得AB=5 6分
法二、设三角形三内角A、B、C对应的三边分别为a, b, c,
∵ ,∴
,∴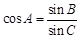 ,由正弦定理有
,由正弦定理有 ,
,
又由余弦定理有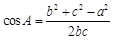 ,∴
,∴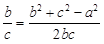 ,即
,即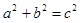 ,
,
所以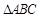 为Rt
为Rt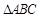 ,且
,且 3分
3分
又
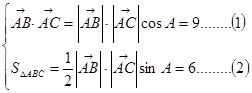
(1)÷(2),得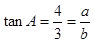 4分
4分
令a="4k," b="3k" (k>0)
则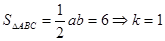 ∴三边长分别为3,4,5 6分
∴三边长分别为3,4,5 6分
(Ⅱ)以C为坐标原点,射线CA为x轴正半轴建立直角坐标系,则A、B坐标为(3,0),(0,4),直线AB方程为
设P点坐标为(x, y),则由P到三边AB、BC、AB的距离为d1, d2和d3可知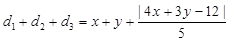 , 8分
, 8分
且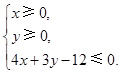 故
故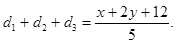 10分
10分
令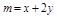 ,由线性规划知识可知0≤m≤8,故d1+d2+d3的取值范围是
,由线性规划知识可知0≤m≤8,故d1+d2+d3的取值范围是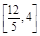 12分
12分
考点:1、解三角形;2、点到直线的距离;3、线性规划

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
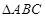 中,角
中,角 、
、 、
、 的对边分别为
的对边分别为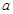 、
、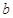 、
、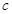 ,且
,且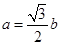 ,
,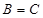 .
.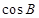 的值;
的值;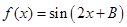 ,求
,求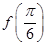 的值.
的值. ,
,
 ,求函数
,求函数 的最大值和最小值,并写出相应的x的值;
的最大值和最小值,并写出相应的x的值; 的内角
的内角 、
、 、
、 的对边分别为
的对边分别为 、
、 、
、 ,满足
,满足 ,
, 且
且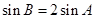 ,求
,求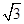 acos C.
acos C.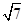 ,且
,且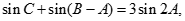 求△ABC的面积.
求△ABC的面积. 中,角
中,角 的对边分别为
的对边分别为 ,且满足
,且满足 .
. 的大小;
的大小; ,求
,求 的最小值.
的最小值.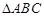 中,角
中,角 、
、 、
、 对的边分别为
对的边分别为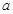 、
、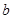 、
、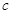 ,且
,且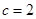 ,
,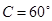 .
.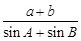 的值;
的值;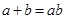 ,求
,求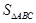 .
. 的周长为
的周长为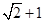 ,且
,且
 的长;
的长; ,求角
,求角 .
. 中,
中, 的对边分别为
的对边分别为 ,若
,若

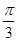 ,BC=2,点D在边AB上,AD=DC,DE⊥AC,E为垂足.
,BC=2,点D在边AB上,AD=DC,DE⊥AC,E为垂足.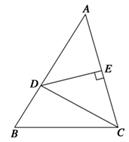
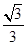 ,求CD的长;
,求CD的长;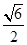 ,求角A的大小.
,求角A的大小.