题目内容
在△ABC中,角A,B,C所对的边分别是a,b,c.己知csin A= 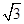 acos C.
acos C.
(I)求C;
(II)若c=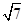 ,且
,且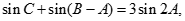 求△ABC的面积.
求△ABC的面积.
(Ⅰ)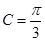 ;(Ⅱ)
;(Ⅱ)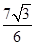 或
或
解析试题分析:(Ⅰ)三角形问题中,涉及边角混合的式子,往往会根据正弦定理或者余弦定理边角转化,或转化为边的式子,利用代数方法处理;或转换为 角的方程,利用三角函数知识处理,该题利用正弦定理转化为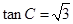 ,再求C;(Ⅱ)已知中含有三个角
,再求C;(Ⅱ)已知中含有三个角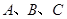 ,观察方程中有
,观察方程中有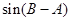 ,利用
,利用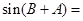
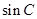 ,转化为两个角的三角方程
,转化为两个角的三角方程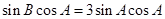 ,然后分
,然后分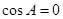 和
和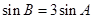 两种情况求三角形面积.
两种情况求三角形面积.
试题解析:(Ⅰ)由正弦定理,得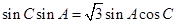 ,因为
,因为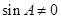 ,解得
,解得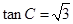 ,
,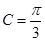 .
.
(Ⅱ)由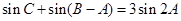 ,得
,得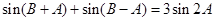 ,
,
整理,得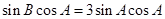 .
.
若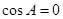 ,则
,则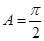 ,
,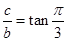 ,
,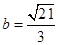 ,
,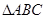 的面积
的面积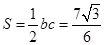
若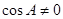 ,则
,则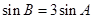 ,
,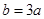 .
.
由余弦定理,得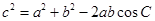 ,解得
,解得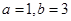 .
.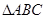 的面积
的面积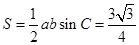 .综上,
.综上,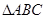 的面积为
的面积为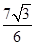 或
或 .
.
考点:1.正弦定理;2.余弦定理;3.三角形面积公式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 中,角
中,角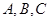 的对边分别为
的对边分别为 ,且满足
,且满足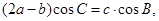
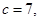
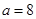 .
.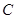 ;
; 中,三个内角
中,三个内角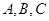 所对边的长分别为
所对边的长分别为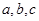 ,已知
,已知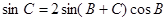 .
.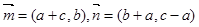 ,若
,若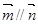 ,求
,求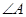 .
. 中内角
中内角 的对边分别为
的对边分别为 ,已知
,已知 ,
, .
. 的值;(2)若
的值;(2)若 为
为 中点,且
中点,且 的面积为
的面积为 ,求
,求 的长度.
的长度.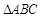 中,已知
中,已知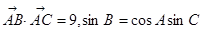 ,又
,又 的面积等于6.
的面积等于6.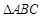 的三边之长;
的三边之长;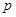 是
是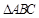 (含边界)内一点,
(含边界)内一点,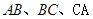 的距离分别为
的距离分别为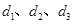 ,求
,求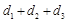 的取值范围.
的取值范围.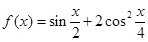
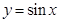 的图像变换得到
的图像变换得到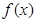 的图像;
的图像;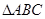 中,角
中,角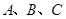 所对的边分别是
所对的边分别是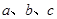 ,若
,若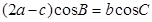 ,求
,求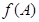 的取值范围
的取值范围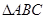 中,设内角
中,设内角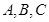 的对边分别为
的对边分别为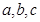 ,向量
,向量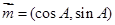 ,向量
,向量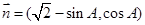 ,若
,若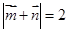
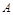 的大小;
的大小;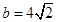 ,且
,且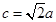 ,求
,求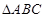 的角
的角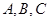 的对边分别为
的对边分别为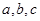 ,已知
,已知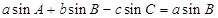 .
.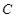 ;
; ,
,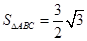 ,求
,求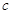 的值.
的值.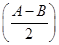 cos B-sin(A-B)sin B+cos(A+C)=-
cos B-sin(A-B)sin B+cos(A+C)=-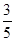 .
. ,b=5,求向量
,b=5,求向量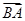 在
在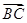 方向上的投影.
方向上的投影.