题目内容
【题目】如图，在四面体ABCD中作截面PQR，若PQ与CB的延长线交于点M，RQ与DB的延长线交于点N，RP与DC的延长线交于点K.
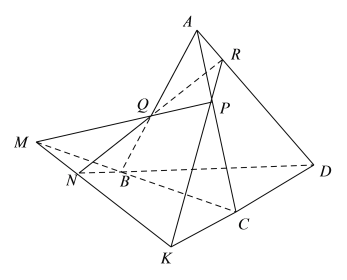
（1）求证：直线
平面PQR；
（2）求证：点K在直线MN上.
【答案】（1）证明见解析；（2）证明见解析
【解析】
（1）根据公理一，证明直线
上有两点在平面PQR上；
（2）根据公理二，证明
都是平面PQR与平面BCD的公共点即可．
证明（1）
平面PQR，
直线PQ，
平面PQR.
平面PQR，
直线RQ，
平面PQR.
直线
平面PQR.
（2）
直线CB，
平面BCD，平面BCD.
由（1）知平面PQR，
在平面PQR与平面BCD的交线上，
同理，可知N，K也在平面PQR与平面BCD的交线上，
，N，K三点共线，
点K在直线MN上.
练习册系列答案
相关题目
