题目内容
平面直角坐标系中, 为原点,射线
为原点,射线 与
与 轴正半轴重合,射线
轴正半轴重合,射线 是第一象限角平分线.在
是第一象限角平分线.在 上有点列
上有点列 ,
, ,在
,在 上有点列
上有点列 ,
, ,
, .已知
.已知 ,
, ,
, .
.

(1)求点 的坐标;
的坐标;
(2)求 的坐标;
的坐标;
(3)求 面积的最大值,并说明理由.
面积的最大值,并说明理由.
 为原点,射线
为原点,射线 与
与 轴正半轴重合,射线
轴正半轴重合,射线 是第一象限角平分线.在
是第一象限角平分线.在 上有点列
上有点列 ,
, ,在
,在 上有点列
上有点列 ,
, ,
, .已知
.已知 ,
, ,
, .
.
(1)求点
 的坐标;
的坐标;(2)求
 的坐标;
的坐标;(3)求
 面积的最大值,并说明理由.
面积的最大值,并说明理由.(1)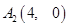 ,
,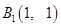 ;(2)
;(2)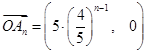 ,
,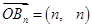 ;(3)
;(3)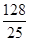 ;
;
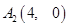 ,
,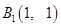 ;(2)
;(2)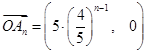 ,
,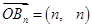 ;(3)
;(3)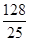 ;
;试题分析:(1)由
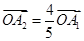 和
和 可求
可求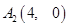 ,由射线
,由射线 是第一象限角平分线和
是第一象限角平分线和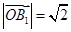 ,利用向量模的公式可求
,利用向量模的公式可求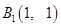 ;(2)设
;(2)设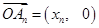 ,
, 可得
可得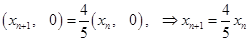
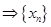 成等比数列,又
成等比数列,又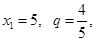 得
得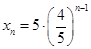 ,进而得到
,进而得到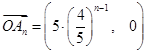 ;设
;设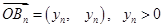 ,得
,得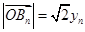 ,由
,由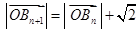 ,得
,得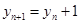 得
得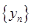 是等差数列,可求得
是等差数列,可求得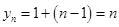 ,进而求得
,进而求得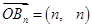 ;(3)由
;(3)由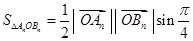 ,可得
,可得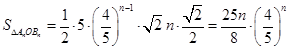 ,利用换元法设
,利用换元法设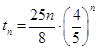 ,当
,当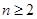 时,
时,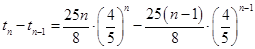 可知
可知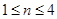 时,
时, 是递增数列,
是递增数列,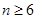 时,
时, 是递减数列,即
是递减数列,即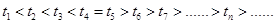 进而求得
进而求得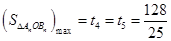 ;
;试题解析:(1)
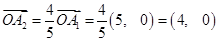 ,
, 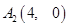 , 2分
, 2分设
 ,由
,由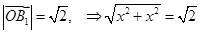 ,
,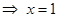 ,∴
,∴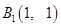 ; 4分
; 4分(2)设
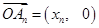 ,则
,则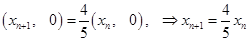 ,
,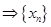 成等比数列, 5分
成等比数列, 5分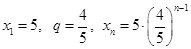 ,∴
,∴ 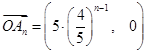 ; 6分
; 6分设
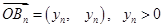 ,
,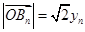 , 7分
, 7分由
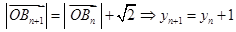 ,
,∴
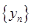 是等差数列, 8分
是等差数列, 8分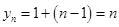 , ∴
, ∴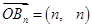 . 9分
. 9分(3)
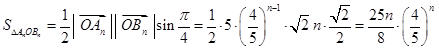 , 11分
, 11分设
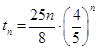 ,
,当
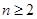 时,
时,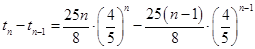
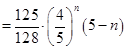 , 12分
, 12分∴
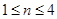 时,
时, 是递增数列,
是递增数列,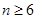 时,
时, 是递减数列,
是递减数列,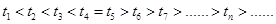 , 13分
, 13分∴
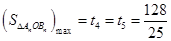 . 14分
. 14分
练习册系列答案
相关题目
 在y轴右侧的交点按横坐标从小到大依次记为P1,P2,…,则
在y轴右侧的交点按横坐标从小到大依次记为P1,P2,…,则 ·
· 等于( )
等于( ) ,
, ,且
,且 ,则 ( )
,则 ( )



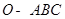 中,点
中,点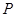 为棱
为棱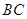 的中点. 设
的中点. 设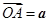 ,
, 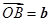 ,
,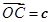 ,那么向量
,那么向量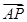 用基底
用基底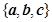 可表示为( )
可表示为( )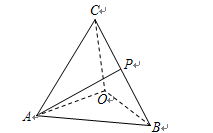




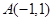 ,点
,点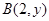 ,向量
,向量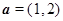 ,若
,若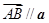 ,则实数
,则实数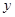 的值为( )
的值为( )
 是第二象限角,
是第二象限角, ,则
,则 = .
= .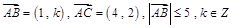 则
则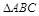 是钝角三角形的概率为 ( )
是钝角三角形的概率为 ( )



 ,
, ,若
,若 ∥
∥ ,则
,则 等于( ).
等于( ).
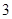


 中,
中, 为边
为边 上任意一点,
上任意一点, 为
为 的中点,
的中点, ,则
,则 的值为( )
的值为( )


