题目内容
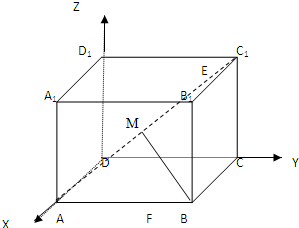如图，在棱长为a的正方体ABCD-A1B1C1D1中，以D为坐标原点，棱DA，DC，DD1为x，y，z轴建立空间直角坐标系，过点B作BM⊥AC1于M，求点M的坐标．
分析：求出
向量，设出M的坐标，利用向量垂直求出M的坐标即可．
| AC1 |
解答：解：由题意可知A（a.0，0），B（a，a，0），C1（0，a，a），∴
=(-a，a，a)，
=λ
，
=
+
=（a（1-λ），λa，λa），
∵BM⊥AC1，∴
•
=0，
（-a，a，a）•（a（1-λ），λa，λa）=0，
可得，-（1-λ）+λ+λ=0，解得λ=
．
M的坐标为（
a，
a，
a）．
| AC1 |
| AM |
| AC1 |
| DM |
| DA |
| AM |
∵BM⊥AC1，∴
| BM |
| AC1 |
（-a，a，a）•（a（1-λ），λa，λa）=0，
可得，-（1-λ）+λ+λ=0，解得λ=
| 1 |
| 3 |
M的坐标为（
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
点评：本题考查空间点的坐标的求法，空间向量数量积的应用，考查计算能力．
练习册系列答案
相关题目
如图，在棱长为2的正四面体A-BCD中，若以△ABC为视角正面，则其正视图的面积是（ ）
，当
取什么位置时，三棱柱的体积最大？
，AG＝
，给出下列四个命题：①AC⊥BD，②FG＝
，③侧面与底面所成二面角的余弦值为
，④
，其中真命题的序号是（ ）
