题目内容
14.设直线l过直线l1:2x-y+1=0与l2:x+y-4=0的交点,且点P(-2,2)到直线l的距离为$\sqrt{5}$,求直线l的方程.分析 联立$\left\{\begin{array}{l}{2x-y+1=0}\\{x+y-4=0}\end{array}\right.$,解得交点M(1,3),由题意可设可设直线l的方程为y-3=k(x-1),利用点到直线的距离公式即可得出.
解答 解:联立$\left\{\begin{array}{l}{2x-y+1=0}\\{x+y-4=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=1}\\{y=3}\end{array}\right.$,可得交点M(1,3),
直线l的斜率不存在时,不满足题意,舍去;
因此可设直线l的方程为y-3=k(x-1),化为kx-y+3-k=0,
∴$\frac{|-2k-2+3-k|}{\sqrt{{k}^{2}+1}}$=$\sqrt{5}$,化为2k2-3k-2=0,解得k=2或-$\frac{1}{2}$.
∴直线l的方程为2x-y+1=0,或x+2y-7=0.
点评 本题考查了直线的交点、点到直线的距离公式,考查了计算能力,属于基础题.

练习册系列答案
相关题目
3.已知f(x)+3f(-x)=2x+1,则f(x)的解析式是( )
| A. | f(x)=x+$\frac{1}{4}$ | B. | f(x)=-2x+$\frac{1}{4}$ | C. | f(x)=-x+$\frac{1}{4}$ | D. | f(x)=-x+$\frac{1}{2}$ |
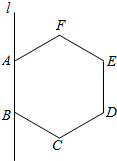 如图所示,ABCDEF是正六边形,将它绕AB所在直线l旋转,画出旋转后的几何体,并指出它是由哪几个简单几何体构成的.
如图所示,ABCDEF是正六边形,将它绕AB所在直线l旋转,画出旋转后的几何体,并指出它是由哪几个简单几何体构成的.