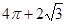题目内容
(本小题满分12分)如图,在直三棱柱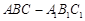 中,
中,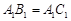 ,
,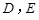 分 别是棱
分 别是棱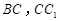 上的点(点
上的点(点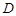 不同于点
不同于点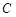 ),且
),且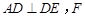 为
为 的中点.
的中点.
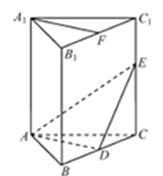
求证:(1)平面 平面
平面 (2)直线
(2)直线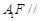 平面
平面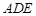
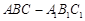 中,
中,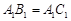 ,
,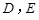 分 别是棱
分 别是棱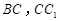 上的点(点
上的点(点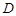 不同于点
不同于点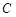 ),且
),且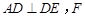 为
为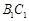 的中点.
的中点.
求证:(1)平面
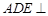 平面
平面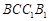 (2)直线
(2)直线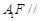 平面
平面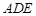
(1)根据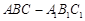 是直三棱柱,则根据其性质可知,
是直三棱柱,则根据其性质可知, 平面
平面 ,然后结合
,然后结合 结合面面垂直的判定定理来得到
结合面面垂直的判定定理来得到
(2)因为 平面
平面 ,那么可知
,那么可知 ,再结合其性质,
,再结合其性质, 平面
平面 。由(1)知,
。由(1)知, 平面
平面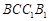 ,可知结论。
,可知结论。
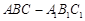 是直三棱柱,则根据其性质可知,
是直三棱柱,则根据其性质可知, 平面
平面 ,然后结合
,然后结合 结合面面垂直的判定定理来得到
结合面面垂直的判定定理来得到(2)因为
 平面
平面 ,那么可知
,那么可知 ,再结合其性质,
,再结合其性质, 平面
平面 。由(1)知,
。由(1)知, 平面
平面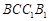 ,可知结论。
,可知结论。试题分析:证明:(1)∵
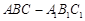 是直三棱柱,∴
是直三棱柱,∴ 平面
平面 。
。又∵
 平面
平面 ,∴
,∴ 。
。又∵
 平面
平面 ,∴
,∴ 平面
平面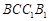 。
。又∵
 平面
平面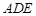 ,∴平面
,∴平面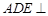 平面
平面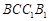 。
。(2)∵
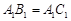 ,
, 为
为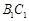 的中点,∴
的中点,∴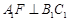 。
。又∵
 平面
平面 ,且
,且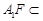 平面
平面 ,∴
,∴ 。
。又∵
 平面
平面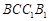 ,
, ,∴
,∴ 平面
平面 。
。由(1)知,
 平面
平面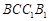 ,∴
,∴ ∥
∥
点评:解决该试题的关键是利用面面垂直和线面垂直的判定定理来加以证明,属于基础题。

练习册系列答案
相关题目
 的底面
的底面 是矩形,
是矩形, ⊥平面
⊥平面 ,
, .
.
 ⊥平面
⊥平面 ;
; 余弦值的大小;
余弦值的大小; 到平面
到平面 的距离.
的距离.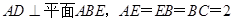 ,F为CE上的点,且BF
,F为CE上的点,且BF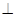 平面ACE,AC与BD交于点G
平面ACE,AC与BD交于点G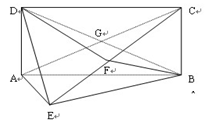
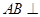 平面
平面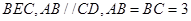 ,
,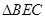 为等边三角形.
为等边三角形.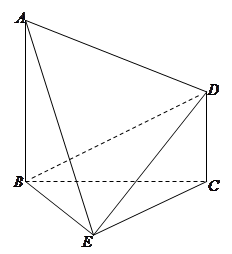
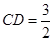 ,求证:平面
,求证:平面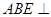 平面
平面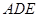 ;
;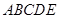 的体积为
的体积为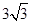 ,求此时二面角
,求此时二面角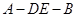 的余弦值.
的余弦值.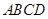 中,
中, 为正三角形,
为正三角形, ,
, ,
, 与
与 交于
交于 点.将
点.将 沿边
沿边 点至
点至 点,已知
点,已知 与平面
与平面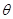 ,且
,且
 平面
平面 ;
; 的余弦值为
的余弦值为 ,求
,求 的大小.
的大小.  中,点
中,点 在线段
在线段 上移动,则异面直线
上移动,则异面直线 与
与 所成的角
所成的角 的取值范围( )
的取值范围( )