题目内容
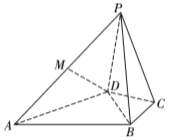
【题目】如图，在三棱柱
中，点
在平面
内运动，使得二面角
的平面角与二面角
的平面角互余，则点的轨迹是( )
A. 一段圆弧 B. 椭圆的一部分 C. 抛物线 D. 双曲线的一支
【答案】D
【解析】
将三棱柱特殊化，看作底面以
为直角的直角三角形，侧棱与底面垂直，然后设出点
的坐标，作出点Q在下底面的投影，由对称性知：点P与点Q的轨迹一致，研究点Q的轨迹即可.
不妨令三棱柱
为直三棱柱，且底面是以为直角的直角三角形，令侧棱长为m,以B的为坐标原点，BA方向为x轴，BC方向为y轴，
方向为z轴，建立空间直角坐标系，
设
，所以
，过点
作以
于点
，作
于点
，
则
即是二面角
的平面角，
即是二面角
的平面角，
所以
，
又二面角的平面角与二面角的平面角互余，所以
，即
，所以
，因，所以
,
所以有
，所以
，即点Q的轨迹是双曲线的一支，所以点的轨迹是双曲线的一支.故选D
练习册系列答案
相关题目
