Question

【题目】已知过抛物线的焦点，斜率为的直线交抛物线于 两点，且.

（1）求该抛物线的方程；

（2）过点任意作互相垂直的两条直线，分别交曲线于点和.设线段的中点分别为，求证：直线恒过一个定点.

Answer 1

【答案】（1）（2见解析

【解析】试题分析： 联立直线方程和抛物线方程，利用弦长公式列方程解出，即可得到抛物线的方程；

设直线的方程，联立抛物线方程得两根之和，计算点的坐标，同理可得点的坐标，运用直线点斜式给出直线方程，讨论斜率问题即可得出定点

解析：（1）抛物线的焦点，∴直线的方程为：

联立方程组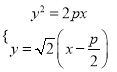，消元得： ，

∴

∴，解得.

∵，∴抛物线的方程为： .

（2）设两点坐标分别为，则点的坐标为..

由题意可设直线的方程为.

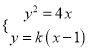由，得.

因为直线与曲线于两点，所以.

所以点的坐标为.

由题知，直线的斜率为，同理可得点的坐标为.

当时，有，此时直线的斜率.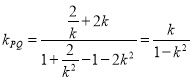

所以，直线的方程为，整理得.

于是，直线恒过定点；

当时，直线的方程为，也过点.

综上所述，直线恒过定点.