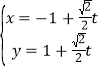题目内容
【题目】已知抛物线
的焦点为
，其准线与
轴交于点
，过点
的直线
与抛物线
交于
，
两点.
（1）求抛物线的方程及
的值；
（2）若点
关于轴的对称点为
，证明：存在实数
，使得
.
【答案】（1）
，4；（2）证明见解析.
【解析】
（1）根据准线上点的坐标，得到
，求出
，即可得到抛物线方程；设直线
的方程为
，联立直线与抛物线方程，由韦达定理，即可求出
；
（2）先由（1）得
，由点
关于
轴的对称点为
，得到
，根据题意，证明直线
恒过定点
，再令
，由
，即可推出结论成立.
（1）解：因为抛物线的准线与轴交于点
，
所以，
解得
.
所以抛物线
的方程为.
设直线的方程为，
联立
整理得
，其中
，
即
.
故
.
（2）证明：由（1）知，
因为点关于轴的对称点为，
所以，
则直线的方程为
，
得
，
得
，
得
，
即
.
令
，得
，
得
，
所以直线恒过定点.
所以点
在线段上，
所以不妨令.
因为，
所以
，
所以
，
所以
.
所以存在实数
，使得
，命题得证.
【题目】阿基米德是古希腊伟大的哲学家、数学家、物理学家，对几何学、力学等学科作出过卓越贡献.为调查中学生对这一伟大科学家的了解程度，某调查小组随机抽取了某市的100名高中生，请他们列举阿基米德的成就，把能列举阿基米德成就不少于3项的称为“比较了解”，少于三项的称为“不太了解”.他们的调查结果如下：
0项 | 1项 | 2项 | 3项 | 4项 | 5项 | 5项以上 | |
理科生（人） | 1 | 10 | 17 | 14 | 14 | 10 | 4 |
文科生（人） | 0 | 8 | 10 | 6 | 3 | 2 | 1 |
（1）完成如下
列联表，并判断是否有
的把握认为，了解阿基米德与选择文理科有关？
比较了解 | 不太了解 | 合计 | |
理科生 | |||
文科生 | |||
合计 |
（2）在抽取的100名高中生中，按照文理科采用分层抽样的方法抽取10人的样本.
（i）求抽取的文科生和理科生的人数；
（ii）从10人的样本中随机抽取3人，用
表示这3人中文科生的人数，求的分布列和数学期望.
参考数据：
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
，
.
