题目内容
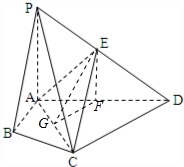
 在四棱锥P-ABCD中,∠ABC═∠ACD=90°,∠BAC=∠CAD=60°,PA⊥底面ABCD,E为PD的中点,PA=2AB=2.
在四棱锥P-ABCD中,∠ABC═∠ACD=90°,∠BAC=∠CAD=60°,PA⊥底面ABCD,E为PD的中点,PA=2AB=2.(1)求四棱锥P-ABCD的体积V;
(2)求二面角E-AC-D的大小.
考点:二面角的平面角及求法,棱柱、棱锥、棱台的体积
专题:计算题,作图题,空间位置关系与距离
分析:(1)将平面ABCD单独拿出来求面积,再求体积即可;
(2)取AD、AC的中点F,G,连结EF,FG,EG;从而可得∠EGF为二面角E-AC-D的平面角,在Rt△EFG中求角.
(2)取AD、AC的中点F,G,连结EF,FG,EG;从而可得∠EGF为二面角E-AC-D的平面角,在Rt△EFG中求角.
解答:
 解:(1)在平面ABCD中,
解:(1)在平面ABCD中,
在Rt△BAC中,
∠ABC═90°,∠BAC=60°,AB=1,
∴BC=
,AC=2;
在Rt△DAC中,
∠ACD═90°,∠CAD=60°,AC=2,
∴CD=2
,AD=4;
故底面ABCD的面积为S=
×1×
+
×2×2
=
;
VP-ABCD=
×S×PA=
×
×2=
.
(2)如图,取AD、AC的中点F,G,
连结EF,FG,EG;
则EF∥PA,
又∵PA⊥底面ABCD,
∴EF⊥底面ABCD,
又∵FG∥CD,CD⊥AC,
∴FG⊥AC,
∴∠EGF为二面角E-AC-D的平面角,
在Rt△EFG中,
EF=
PA=1,GF=
CD=
,
∴tan∠EGF=
=
,
∴∠EGF=30°;
即二面角E-AC-D的大小为30°.
 解:(1)在平面ABCD中,
解:(1)在平面ABCD中,在Rt△BAC中,
∠ABC═90°,∠BAC=60°,AB=1,
∴BC=
| 3 |
在Rt△DAC中,
∠ACD═90°,∠CAD=60°,AC=2,
∴CD=2
| 3 |
故底面ABCD的面积为S=
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
5
| ||
| 2 |
VP-ABCD=
| 1 |
| 3 |
| 1 |
| 3 |
5
| ||
| 2 |
5
| ||
| 3 |
(2)如图,取AD、AC的中点F,G,
连结EF,FG,EG;
则EF∥PA,
又∵PA⊥底面ABCD,
∴EF⊥底面ABCD,
又∵FG∥CD,CD⊥AC,
∴FG⊥AC,
∴∠EGF为二面角E-AC-D的平面角,
在Rt△EFG中,
EF=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
∴tan∠EGF=
| EF |
| GF |
| ||
| 3 |
∴∠EGF=30°;
即二面角E-AC-D的大小为30°.
点评:本题考查了学生的空间想象力及计算能力,属于中档题.

练习册系列答案
相关题目
正四面体棱长为1,其外接球的表面积为( )
A、
| ||
| B、π | ||
C、
| ||
| D、3π |
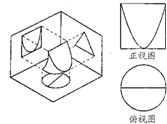 一个圆柱从顶部切掉两块,剩下部分几何体如图所示,此几何体的正视图和俯视图如图所示,其中正视图中的四边形是边长为2的正方形,则此几何体的侧视图的面积为( )
一个圆柱从顶部切掉两块,剩下部分几何体如图所示,此几何体的正视图和俯视图如图所示,其中正视图中的四边形是边长为2的正方形,则此几何体的侧视图的面积为( )